Optimization of phase-only holograms calculated with scaled diffraction calculation through deep neural networks

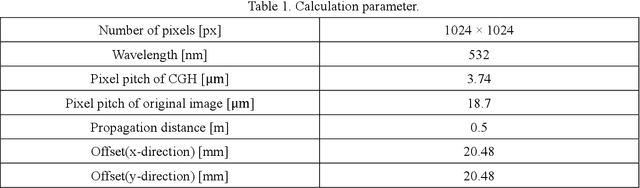
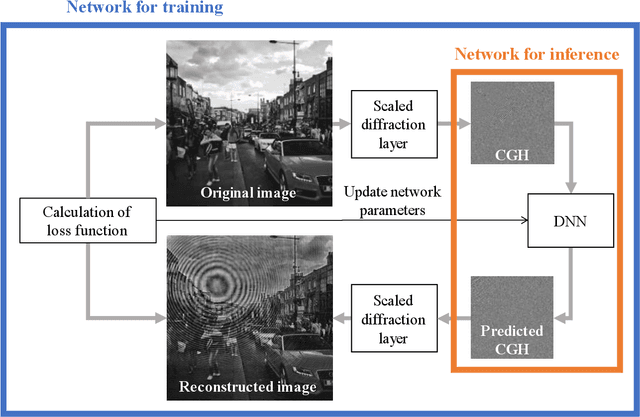
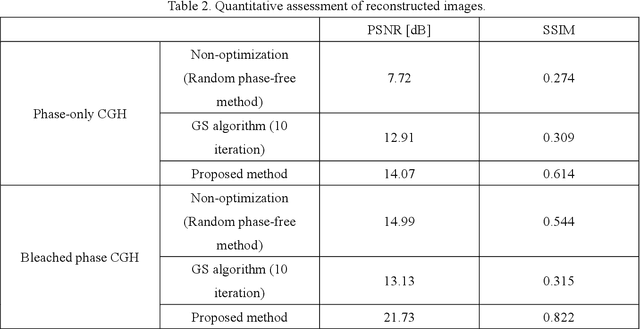
Computer-generated holograms (CGHs) are used in holographic three-dimensional (3D) displays and holographic projections. The quality of the reconstructed images using phase-only CGHs is degraded because the amplitude of the reconstructed image is difficult to control. Iterative optimization methods such as the Gerchberg-Saxton (GS) algorithm are one option for improving image quality. They optimize CGHs in an iterative fashion to obtain a higher image quality. However, such iterative computation is time consuming, and the improvement in image quality is often stagnant. Recently, deep learning-based hologram computation has been proposed. Deep neural networks directly infer CGHs from input image data. However, it is limited to reconstructing images that are the same size as the hologram. In this study, we use deep learning to optimize phase-only CGHs generated using scaled diffraction computations and the random phase-free method. By combining the random phase-free method with the scaled diffraction computation, it is possible to handle a zoomable reconstructed image larger than the hologram. In comparison to the GS algorithm, the proposed method optimizes both high quality and speed.

From Adaptive Kernel Density Estimation to Sparse Mixture Models

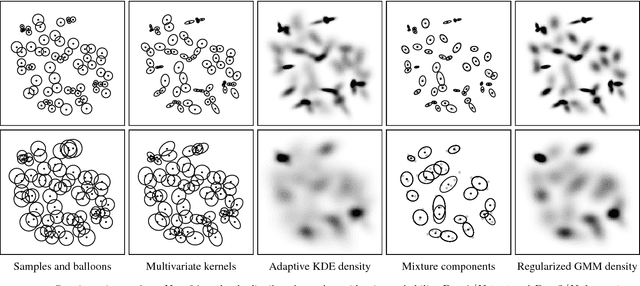
We introduce a balloon estimator in a generalized expectation-maximization method for estimating all parameters of a Gaussian mixture model given one data sample per mixture component. Instead of limiting explicitly the model size, this regularization strategy yields low-complexity sparse models where the number of effective mixture components reduces with an increase of a smoothing probability parameter $\mathbf{P>0}$. This semi-parametric method bridges from non-parametric adaptive kernel density estimation (KDE) to parametric ordinary least-squares when $\mathbf{P=1}$. Experiments show that simpler sparse mixture models retain the level of details present in the adaptive KDE solution.