From Adaptive Kernel Density Estimation to Sparse Mixture Models
Paper and Code
Dec 11, 2018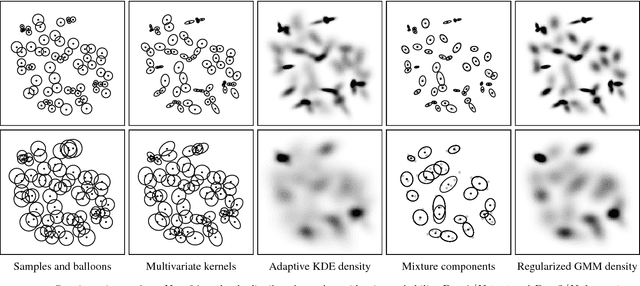
We introduce a balloon estimator in a generalized expectation-maximization method for estimating all parameters of a Gaussian mixture model given one data sample per mixture component. Instead of limiting explicitly the model size, this regularization strategy yields low-complexity sparse models where the number of effective mixture components reduces with an increase of a smoothing probability parameter $\mathbf{P>0}$. This semi-parametric method bridges from non-parametric adaptive kernel density estimation (KDE) to parametric ordinary least-squares when $\mathbf{P=1}$. Experiments show that simpler sparse mixture models retain the level of details present in the adaptive KDE solution.
* in Proceedings of iTWIST'18, Paper-ID: 20, Marseille, France,
November, 21-23, 2018
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge