Peter Kling
Symmetry Preservation in Swarms of Oblivious Robots with Limited Visibility
Sep 28, 2024Abstract:In the general pattern formation (GPF) problem, a swarm of simple autonomous, disoriented robots must form a given pattern. The robots' simplicity imply a strong limitation: When the initial configuration is rotationally symmetric, only patterns with a similar symmetry can be formed [Yamashita, Suzyuki; TCS 2010]. The only known algorithm to form large patterns with limited visibility and without memory requires the robots to start in a near-gathering (a swarm of constant diameter) [Hahn et al.; SAND 2024]. However, not only do we not know any near-gathering algorithm guaranteed to preserve symmetry but most natural gathering strategies trivially increase symmetries [Castenow et al.; OPODIS 2022]. Thus, we study near-gathering without changing the swarm's rotational symmetry for disoriented, oblivious robots with limited visibility (the OBLOT-model, see [Flocchini et al.; 2019]). We introduce a technique based on the theory of dynamical systems to analyze how a given algorithm affects symmetry and provide sufficient conditions for symmetry preservation. Until now, it was unknown whether the considered OBLOT-model allows for any non-trivial algorithm that always preserves symmetry. Our first result shows that a variant of Go-to-the-Average always preserves symmetry but may sometimes lead to multiple, unconnected near-gathering clusters. Our second result is a symmetry-preserving near-gathering algorithm that works on swarms with a convex boundary (the outer boundary of the unit disc graph) and without holes (circles of diameter 1 inside the boundary without any robots).
Forming Large Patterns with Local Robots in the OBLOT Model
Apr 04, 2024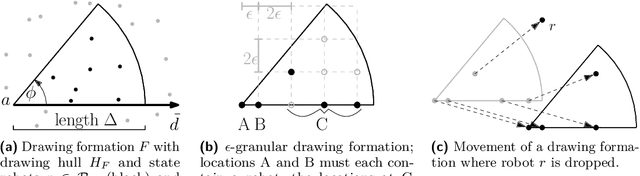
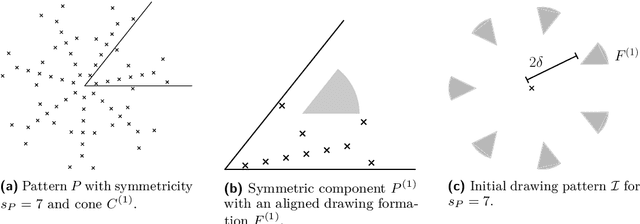
Abstract:In the arbitrary pattern formation problem, $n$ autonomous, mobile robots must form an arbitrary pattern $P \subseteq \mathbb{R}^2$. The (deterministic) robots are typically assumed to be indistinguishable, disoriented, and unable to communicate. An important distinction is whether robots have memory and/or a limited viewing range. Previous work managed to form $P$ under a natural symmetry condition if robots have no memory but an unlimited viewing range [22] or if robots have a limited viewing range but memory [25]. In the latter case, $P$ is only formed in a shrunk version that has constant diameter. Without memory and with limited viewing range, forming arbitrary patterns remains an open problem. We provide a partial solution by showing that $P$ can be formed under the same symmetry condition if the robots' initial diameter is $\leq 1$. Our protocol partitions $P$ into rotation-symmetric components and exploits the initial mutual visibility to form one cluster per component. Using a careful placement of the clusters and their robots, we show that a cluster can move in a coordinated way through its component while drawing $P$ by dropping one robot per pattern coordinate.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge