Pendar Alirezazadeh
A Quadruplet Loss for Enforcing Semantically Coherent Embeddings in Multi-output Classification Problems
Mar 20, 2020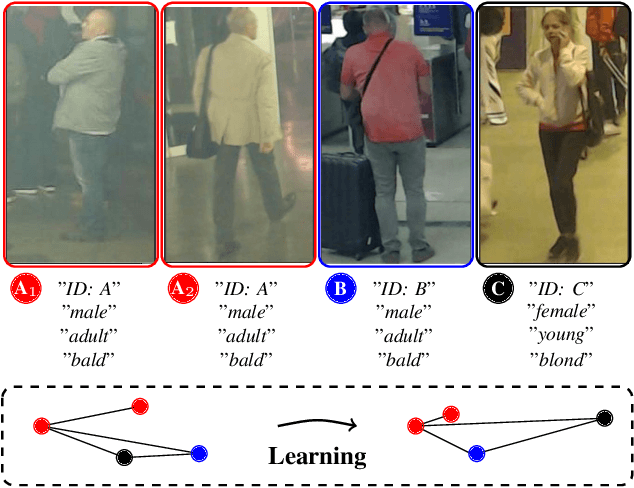
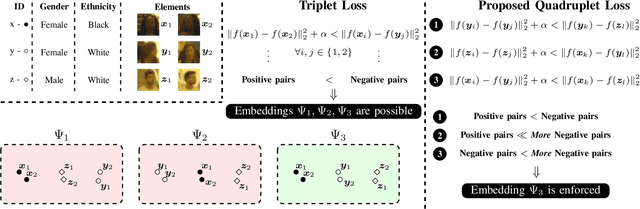
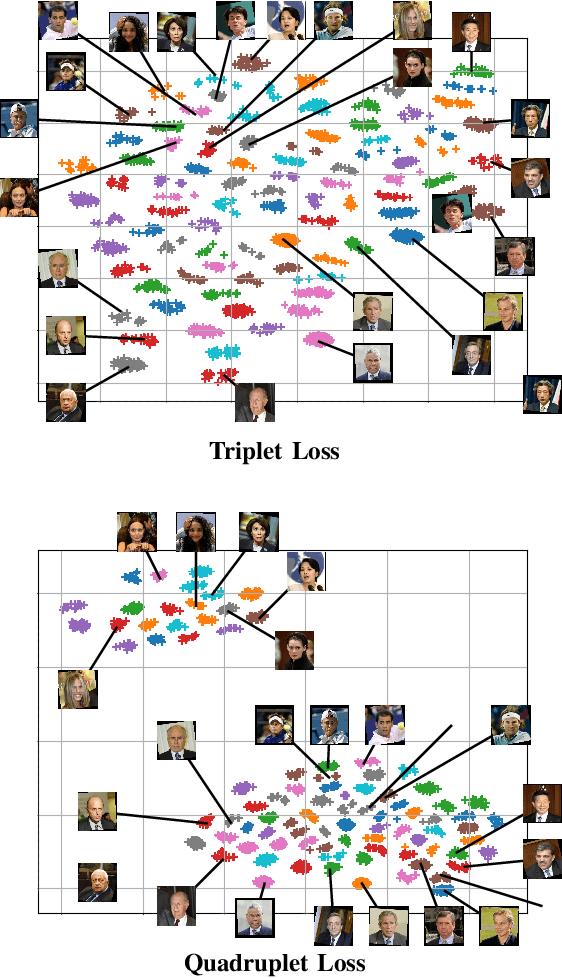
Abstract:This paper describes one objective function for learning semantically coherent feature embeddings in multi-output classification problems, i.e., when the response variables have dimension higher than one. In particular, we consider the problems of identity retrieval and soft biometrics labelling in visual surveillance environments, which have been attracting growing interests. Inspired by the triplet loss [34] function, we propose a generalization that: 1) defines a metric that considers the number of agreeing labels between pairs of elements; and 2) disregards the notion of anchor, replacing d(A1, A2) < d(A1, B) by d(A, B) < d(C, D), for A, B, C, D distance constraints, according to the number of agreeing labels between pairs. As the triplet loss formulation, our proposal also privileges small distances between positive pairs, but at the same time explicitly enforces that the distance between other pairs corresponds directly to their similarity in terms of agreeing labels. This yields feature embeddings with a strong correspondence between the classes centroids and their semantic descriptions, i.e., where elements are closer to others that share some of their labels than to elements with fully disjoint labels membership. As practical effect, the proposed loss can be seen as particularly suitable for performing joint coarse (soft label) + fine (ID) inference, based on simple rules as k-neighbours, which is a novelty with respect to previous related loss functions. Also, in opposition to its triplet counterpart, the proposed loss is agnostic with regard to any demanding criteria for mining learning instances (such as the semi-hard pairs). Our experiments were carried out in five different datasets (BIODI, LFW, IJB-A, Megaface and PETA) and validate our assumptions, showing highly promising results.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge