RadioDiff-Flux: Efficient Radio Map Construction via Generative Denoise Diffusion Model Trajectory Midpoint Reuse

Accurate radio map (RM) construction is essential to enabling environment-aware and adaptive wireless communication. However, in future 6G scenarios characterized by high-speed network entities and fast-changing environments, it is very challenging to meet real-time requirements. Although generative diffusion models (DMs) can achieve state-of-the-art accuracy with second-level delay, their iterative nature leads to prohibitive inference latency in delay-sensitive scenarios. In this paper, by uncovering a key structural property of diffusion processes: the latent midpoints remain highly consistent across semantically similar scenes, we propose RadioDiff-Flux, a novel two-stage latent diffusion framework that decouples static environmental modeling from dynamic refinement, enabling the reuse of precomputed midpoints to bypass redundant denoising. In particular, the first stage generates a coarse latent representation using only static scene features, which can be cached and shared across similar scenarios. The second stage adapts this representation to dynamic conditions and transmitter locations using a pre-trained model, thereby avoiding repeated early-stage computation. The proposed RadioDiff-Flux significantly reduces inference time while preserving fidelity. Experiment results show that RadioDiff-Flux can achieve up to 50 acceleration with less than 0.15% accuracy loss, demonstrating its practical utility for fast, scalable RM generation in future 6G networks.

Erasing Noise in Signal Detection with Diffusion Model: From Theory to Application

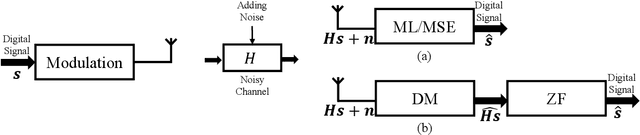
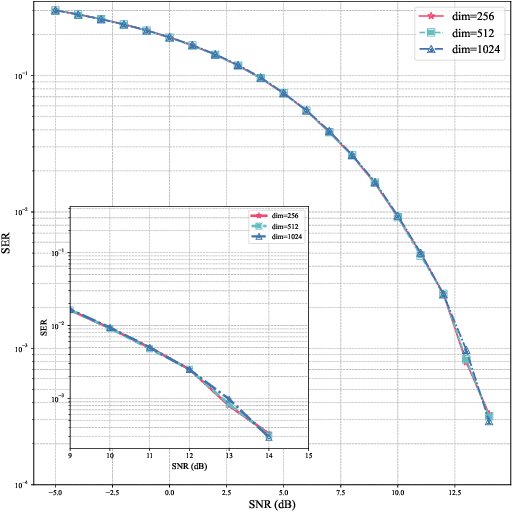
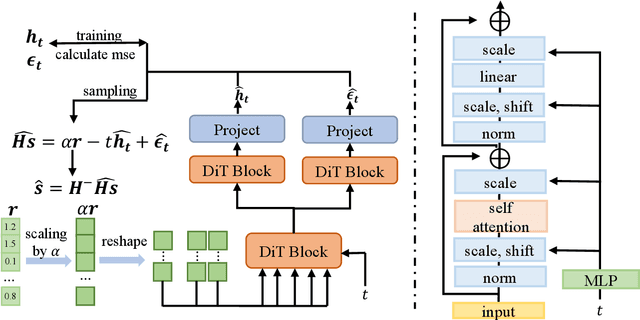
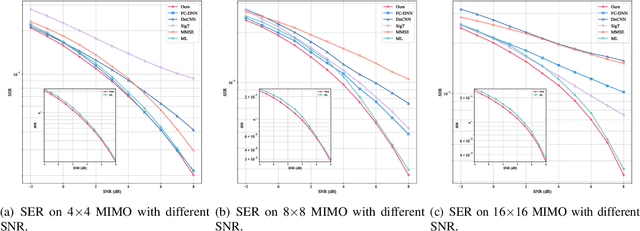
In this paper, a signal detection method based on the denoise diffusion model (DM) is proposed, which outperforms the maximum likelihood (ML) estimation method that has long been regarded as the optimal signal detection technique. Theoretically, a novel mathematical theory for intelligent signal detection based on stochastic differential equations (SDEs) is established in this paper, demonstrating the effectiveness of DM in reducing the additive white Gaussian noise in received signals. Moreover, a mathematical relationship between the signal-to-noise ratio (SNR) and the timestep in DM is established, revealing that for any given SNR, a corresponding optimal timestep can be identified. Furthermore, to address potential issues with out-of-distribution inputs in the DM, we employ a mathematical scaling technique that allows the trained DM to handle signal detection across a wide range of SNRs without any fine-tuning. Building on the above theoretical foundation, we propose a DM-based signal detection method, with the diffusion transformer (DiT) serving as the backbone neural network, whose computational complexity of this method is $\mathcal{O}(n^2)$. Simulation results demonstrate that, for BPSK and QAM modulation schemes, the DM-based method achieves a significantly lower symbol error rate (SER) compared to ML estimation, while maintaining a much lower computational complexity.