More Efficient Identifiability Verification in ODE Models by Reducing Non-Identifiability

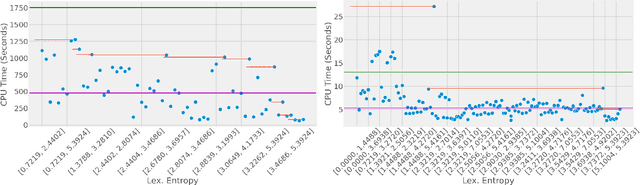
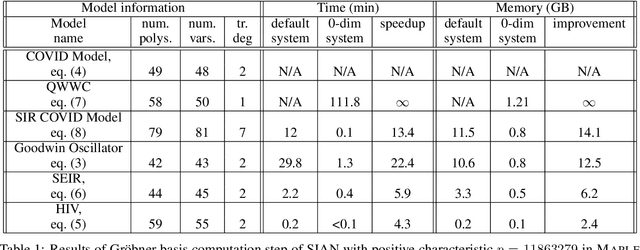
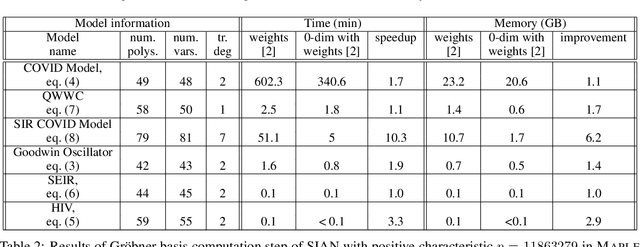
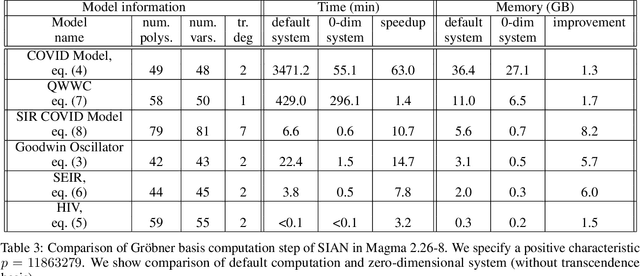
Structural global parameter identifiability indicates whether one can determine a parameter's value from given inputs and outputs in the absence of noise. If a given model has parameters for which there may be infinitely many values, such parameters are called non-identifiable. We present a procedure for accelerating a global identifiability query by eliminating algebraically independent non-identifiable parameters. Our proposed approach significantly improves performance across different computer algebra frameworks.

Locally Random P-adic Alloy Codes with Channel Coding Theorems for Distributed Coded Tensors

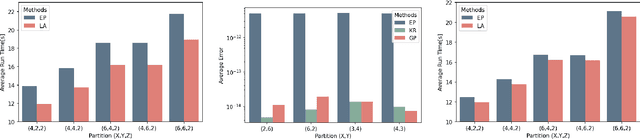
Tensors, i.e., multi-linear functions, are a fundamental building block of machine learning algorithms. In order to train on large data-sets, it is common practice to distribute the computation amongst workers. However, stragglers and other faults can severely impact the performance and overall training time. A novel strategy to mitigate these failures is the use of coded computation. We introduce a new metric for analysis called the typical recovery threshold, which focuses on the most likely event and provide a novel construction of distributed coded tensor operations which are optimal with this measure. We show that our general framework encompasses many other computational schemes and metrics as a special case. In particular, we prove that the recovery threshold and the tensor rank can be recovered as a special case of the typical recovery threshold when the probability of noise, i.e., a fault, is equal to zero, thereby providing a noisy generalization of noiseless computation as a serendipitous result. Far from being a purely theoretical construction, these definitions lead us to practical random code constructions, i.e., locally random p-adic alloy codes, which are optimal with respect to the measures. We analyze experiments conducted on Amazon EC2 and establish that they are faster and more numerically stable than many other benchmark computation schemes in practice, as is predicted by theory.

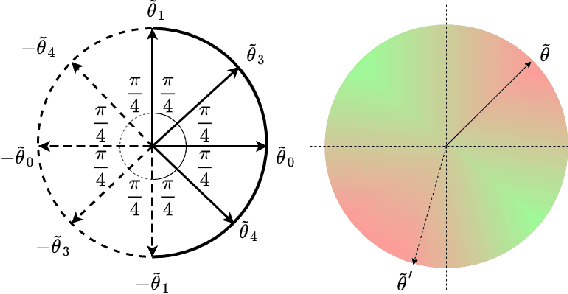
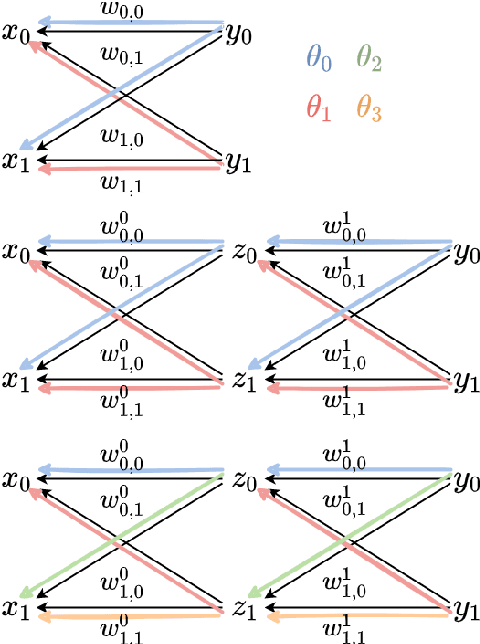
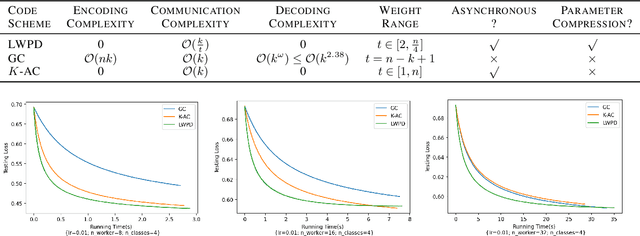
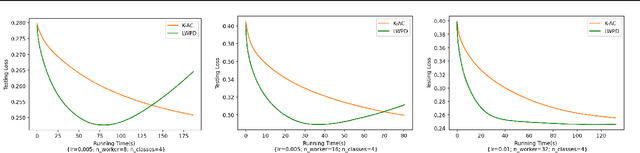
Lightweight Projective Derivative Codes for Compressed Asynchronous Gradient Descent

Coded distributed computation has become common practice for performing gradient descent on large datasets to mitigate stragglers and other faults. This paper proposes a novel algorithm that encodes the partial derivatives themselves and furthermore optimizes the codes by performing lossy compression on the derivative codewords by maximizing the information contained in the codewords while minimizing the information between the codewords. The utility of this application of coding theory is a geometrical consequence of the observed fact in optimization research that noise is tolerable, sometimes even helpful, in gradient descent based learning algorithms since it helps avoid overfitting and local minima. This stands in contrast with much current conventional work on distributed coded computation which focuses on recovering all of the data from the workers. A second further contribution is that the low-weight nature of the coding scheme allows for asynchronous gradient updates since the code can be iteratively decoded; i.e., a worker's task can immediately be updated into the larger gradient. The directional derivative is always a linear function of the direction vectors; thus, our framework is robust since it can apply linear coding techniques to general machine learning frameworks such as deep neural networks.