Time-efficient filtering of polarimetric data by checking physical realizability of experimental Mueller matrices

Imaging Mueller polarimetry has already proved its potential for metrology, remote sensing and biomedicine. The real-time applications of this modality require both video rate image acquisition and fast data post-processing algorithms. First, one must check the physical realizability of the experimental Mueller matrices in order to filter out non-physical data, i.e. to test the positive semi-definiteness of the 4x4 Hermitian coherency matrix calculated from the elements of the corresponding Mueller matrix pixel-wise. For this purpose, we compared the execution time for the calculations of i) eigenvalues, ii) Cholesky decomposition, iii) Sylvester's criterion, and iv) coefficients of the characteristic polynomial of the Hermitian coherency matrix using two different approaches, all calculated for the experimental Mueller matrix images (600 pixels x 700 pixels) of mouse uterine cervix. The calculations were performed using C++ and Julia programming languages. Our results showed the superiority of the algorithm iv), in particular, the version based on the simplification via Pauli matrices, in terms of execution time for our dataset, over other algorithms. The sequential implementation of the latter algorithm on a single core already satisfies the requirements of real-time polarimetric imaging in various domains. This can be further amplified by the proposed parallelization (for example, we achieve a 5-fold speed up on 6 cores).

More Efficient Identifiability Verification in ODE Models by Reducing Non-Identifiability

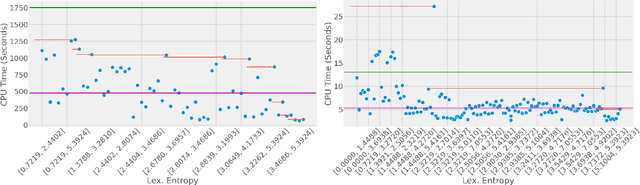
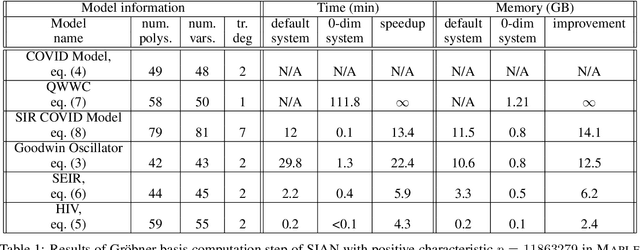
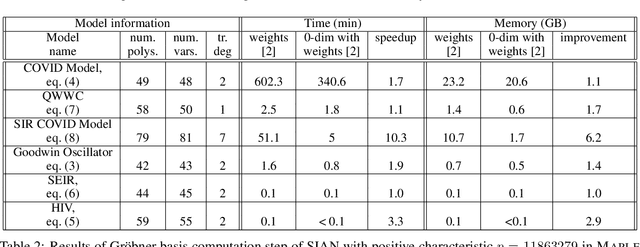
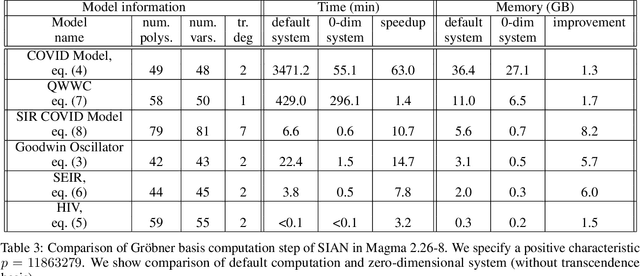
Structural global parameter identifiability indicates whether one can determine a parameter's value from given inputs and outputs in the absence of noise. If a given model has parameters for which there may be infinitely many values, such parameters are called non-identifiable. We present a procedure for accelerating a global identifiability query by eliminating algebraically independent non-identifiable parameters. Our proposed approach significantly improves performance across different computer algebra frameworks.