Audio Decoding by Inverse Problem Solving

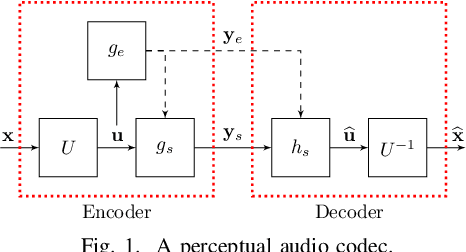
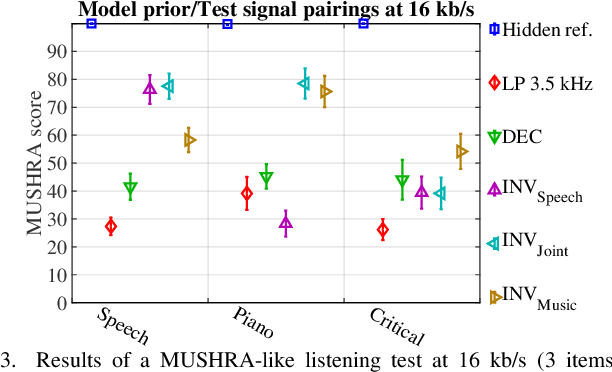
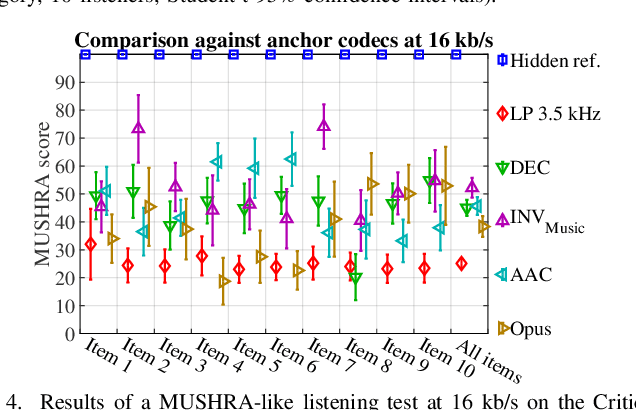
We consider audio decoding as an inverse problem and solve it through diffusion posterior sampling. Explicit conditioning functions are developed for input signal measurements provided by an example of a transform domain perceptual audio codec. Viability is demonstrated by evaluating arbitrary pairings of a set of bitrates and task-agnostic prior models. For instance, we observe significant improvements on piano while maintaining speech performance when a speech model is replaced by a joint model trained on both speech and piano. With a more general music model, improved decoding compared to legacy methods is obtained for a broad range of content types and bitrates. The noisy mean model, underlying the proposed derivation of conditioning, enables a significant reduction of gradient evaluations for diffusion posterior sampling, compared to methods based on Tweedie's mean. Combining Tweedie's mean with our conditioning functions improves the objective performance. An audio demo is available at https://dpscodec-demo.github.io/.

Distribution Preserving Source Separation With Time Frequency Predictive Models

We provide an example of a distribution preserving source separation method, which aims at addressing perceptual shortcomings of state-of-the-art methods. Our approach uses unconditioned generative models of signal sources. Reconstruction is achieved by means of mix-consistent sampling from a distribution conditioned on a realization of a mix. The separated signals follow their respective source distributions, which provides an advantage when separation results are evaluated in a listening test.

Exact multiplicative updates for convolutional $β$-NMF in 2D

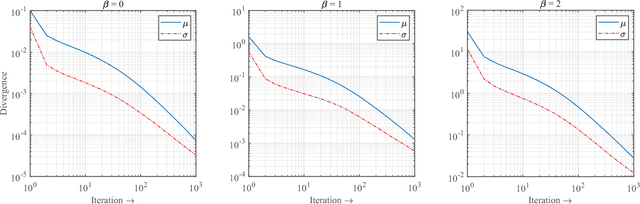
In this paper, we extend the $\beta$-CNMF to two dimensions and derive exact multiplicative updates for its factors. The new updates generalize and correct the nonnegative matrix factor deconvolution previously proposed by Schmidt and M{\o}rup. We show by simulation that the updates lead to a monotonically decreasing $\beta$-divergence in terms of the mean and the standard deviation and that the corresponding convergence curves are consistent across the most common values for $\beta$.

Multiplicative Updates for Convolutional NMF Under $β$-Divergence

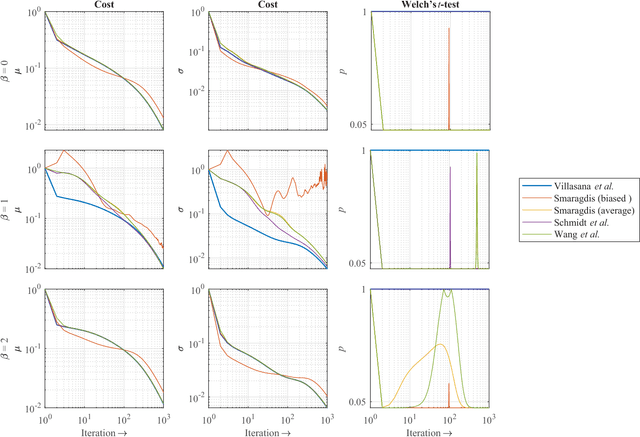
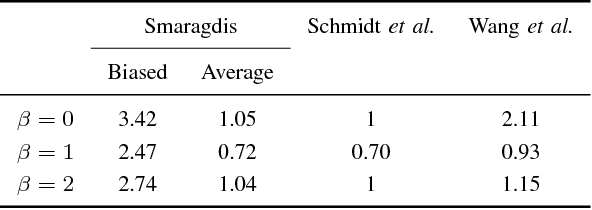
In this letter, we generalize the convolutional NMF by taking the $\beta$-divergence as the contrast function and present the correct multiplicative updates for its factors in closed form. The new updates unify the $\beta$-NMF and the convolutional NMF. We state why almost all of the existing updates are inexact and approximative w.r.t. the convolutional data model. We show that our updates are stable and that their convergence performance is consistent across the most common values of $\beta$.