Pawanesh Yadav
Uncovering the hidden core-periphery structure in hyperbolic networks
Jun 28, 2024
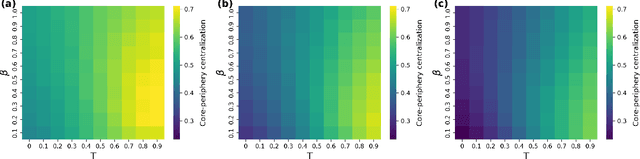
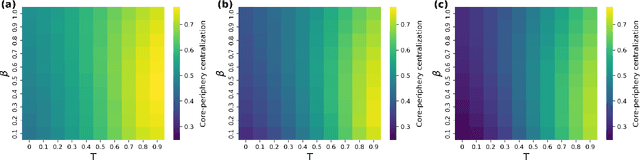
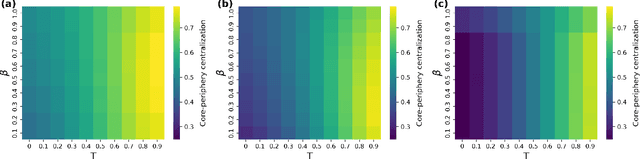
Abstract:The hyperbolic network models exhibit very fundamental and essential features, like small-worldness, scale-freeness, high-clustering coefficient, and community structure. In this paper, we comprehensively explore the presence of an important feature, the core-periphery structure, in the hyperbolic network models, which is often exhibited by real-world networks. We focused on well-known hyperbolic models such as popularity-similarity optimization model (PSO) and S1/H2 models and studied core-periphery structures using a well-established method that is based on standard random walk Markov chain model. The observed core-periphery centralization values indicate that the core-periphery structure can be very pronounced under certain conditions. We also validate our findings by statistically testing for the significance of the observed core-periphery structure in the network geometry. This study extends network science and reveals core-periphery insights applicable to various domains, enhancing network performance and resiliency in transportation and information systems.
Explaining Indian Stock Market through Geometry of Scale free Networks
Apr 06, 2024
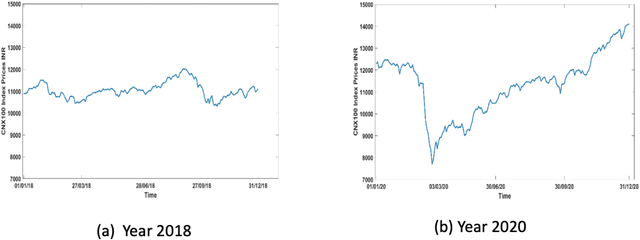

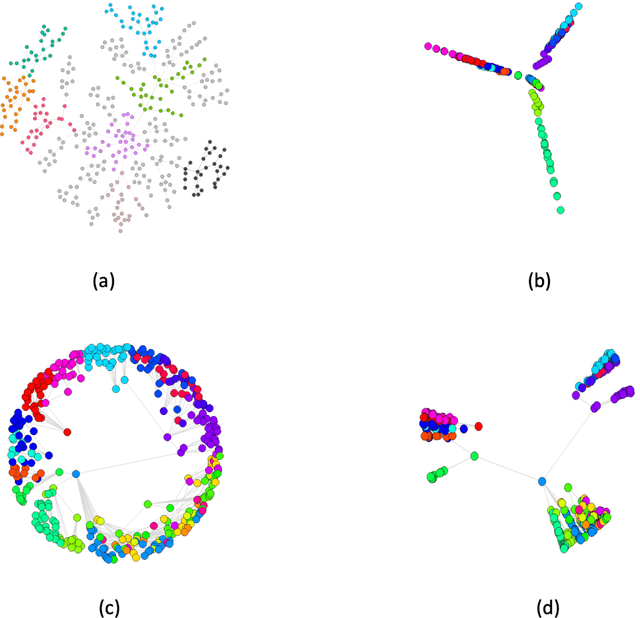
Abstract:This paper presents an analysis of the Indian stock market using a method based on embedding the network in a hyperbolic space using Machine learning techniques. We claim novelty on four counts. First, it is demonstrated that the hyperbolic clusters resemble the topological network communities more closely than the Euclidean clusters. Second, we are able to clearly distinguish between periods of market stability and volatility through a statistical analysis of hyperbolic distance and hyperbolic shortest path distance corresponding to the embedded network. Third, we demonstrate that using the modularity of the embedded network significant market changes can be spotted early. Lastly, the coalescent embedding is able to segregate the certain market sectors thereby underscoring its natural clustering ability.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge