Dissecting graph measure performance for node clustering in LFR parameter space

Graph measures that express closeness or distance between nodes can be employed for graph nodes clustering using metric clustering algorithms. There are numerous measures applicable to this task, and which one performs better is an open question. We study the performance of 25 graph measures on generated graphs with different parameters. While usually measure comparisons are limited to general measure ranking on a particular dataset, we aim to explore the performance of various measures depending on graph features. Using an LFR graph generator, we create a dataset of 11780 graphs covering the whole LFR parameter space. For each graph, we assess the quality of clustering with k-means algorithm for each considered measure. Based on this, we determine the best measure for each area of the parameter space. We find that the parameter space consists of distinct zones where one particular measure is the best. We analyze the geometry of the resulting zones and describe it with simple criteria. Given particular graph parameters, this allows us to recommend a particular measure to use for clustering.

How to choose the most appropriate centrality measure?

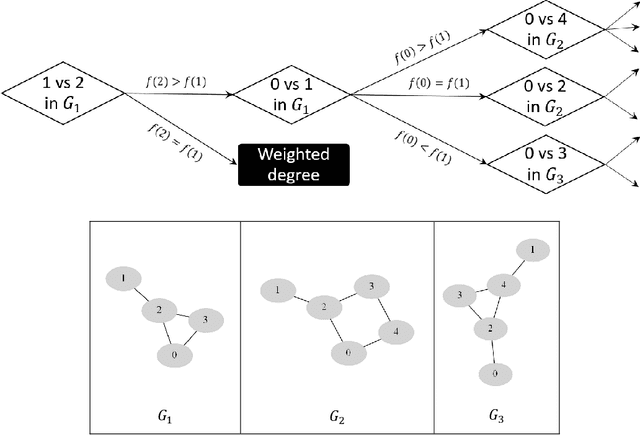
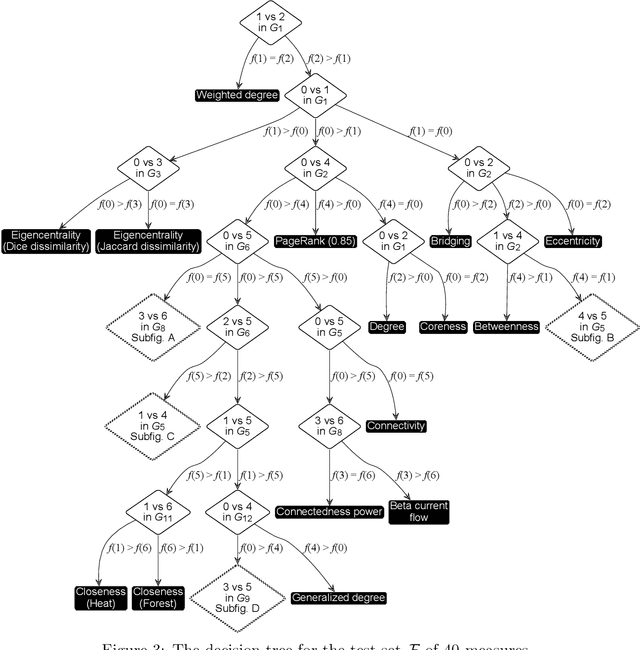
We propose a new method to select the most appropriate network centrality measure based on the user's opinion on how such a measure should work on a set of simple graphs. The method consists in: (1) forming a set $\cal F$ of candidate measures; (2) generating a sequence of sufficiently simple graphs that distinguish all measures in $\cal F$ on some pairs of nodes; (3) compiling a survey with questions on comparing the centrality of test nodes; (4) completing this survey, which provides a centrality measure consistent with all user responses. The developed algorithms make it possible to implement this approach for any finite set $\cal F$ of measures. This paper presents its realization for a set of 40 centrality measures. The proposed method called culling can be used for rapid analysis or combined with a normative approach by compiling a survey on the subset of measures that satisfy certain normative conditions (axioms). In the present study, the latter was done for the subsets determined by the Self-consistency or Bridge axioms.

Do logarithmic proximity measures outperform plain ones in graph clustering?

We consider a number of graph kernels and proximity measures including commute time kernel, regularized Laplacian kernel, heat kernel, exponential diffusion kernel (also called "communicability"), etc., and the corresponding distances as applied to clustering nodes in random graphs and several well-known datasets. The model of generating random graphs involves edge probabilities for the pairs of nodes that belong to the same class or different predefined classes of nodes. It turns out that in most cases, logarithmic measures (i.e., measures resulting after taking logarithm of the proximities) perform better while distinguishing underlying classes than the "plain" measures. A comparison in terms of reject curves of inter-class and intra-class distances confirms this conclusion. A similar conclusion can be made for several well-known datasets. A possible origin of this effect is that most kernels have a multiplicative nature, while the nature of distances used in cluster algorithms is an additive one (cf. the triangle inequality). The logarithmic transformation is a tool to transform the first nature to the second one. Moreover, some distances corresponding to the logarithmic measures possess a meaningful cutpoint additivity property. In our experiments, the leader is usually the logarithmic Communicability measure. However, we indicate some more complicated cases in which other measures, typically, Communicability and plain Walk, can be the winners.

Semi-supervised Learning with Regularized Laplacian

We study a semi-supervised learning method based on the similarity graph and RegularizedLaplacian. We give convenient optimization formulation of the Regularized Laplacian method and establishits various properties. In particular, we show that the kernel of the methodcan be interpreted in terms of discrete and continuous time random walks and possesses several importantproperties of proximity measures. Both optimization and linear algebra methods can be used for efficientcomputation of the classification functions. We demonstrate on numerical examples that theRegularized Laplacian method is competitive with respect to the other state of the art semi-supervisedlearning methods.

Matrices of forests, analysis of networks, and ranking problems

The matrices of spanning rooted forests are studied as a tool for analysing the structure of networks and measuring their properties. The problems of revealing the basic bicomponents, measuring vertex proximity, and ranking from preference relations / sports competitions are considered. It is shown that the vertex accessibility measure based on spanning forests has a number of desirable properties. An interpretation for the stochastic matrix of out-forests in terms of information dissemination is given.

Matrices of Forests and the Analysis of Digraphs

The matrices of spanning rooted forests are studied as a tool for analysing the structure of digraphs and measuring their characteristics. The problems of revealing the basis bicomponents, measuring vertex proximity, and ranking from preference relations / sports competitions are considered. It is shown that the vertex accessibility measure based on spanning forests has a number of desirable properties. An interpretation for the normalized matrix of out-forests in terms of information dissemination is given. Keywords: Laplacian matrix, spanning forest, matrix-forest theorem, proximity measure, bicomponent, ranking, incomplete tournament, paired comparisons