Patrick Zhong
Optimizing pre-scheduled, intermittently-observed MDPs
May 16, 2023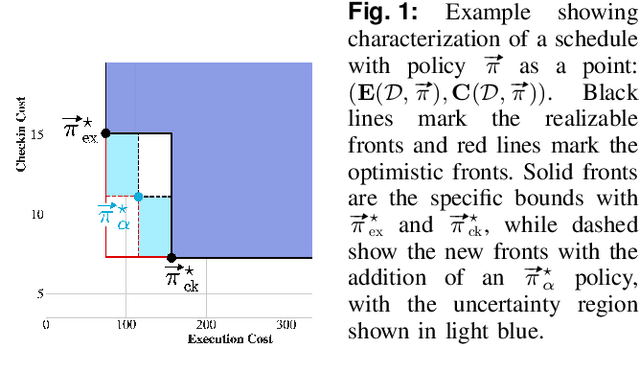
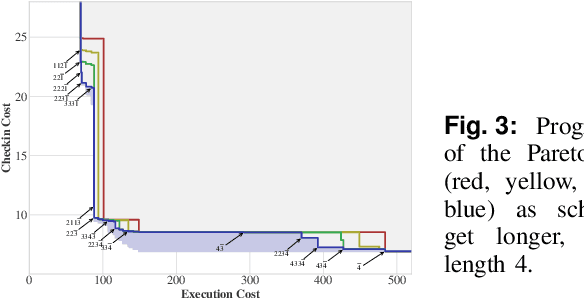

Abstract:A challenging category of robotics problems arises when sensing incurs substantial costs. This paper examines settings in which a robot wishes to limit its observations of state, for instance, motivated by specific considerations of energy management, stealth, or implicit coordination. We formulate the problem of planning under uncertainty when the robot's observations are intermittent but their timing is known via a pre-declared schedule. After having established the appropriate notion of an optimal policy for such settings, we tackle the problem of joint optimization of the cumulative execution cost and the number of state observations, both in expectation under discounts. To approach this multi-objective optimization problem, we introduce an algorithm that can identify the Pareto front for a class of schedules that are advantageous in the discounted setting. The algorithm proceeds in an accumulative fashion, prepending additions to a working set of schedules and then computing incremental changes to the value functions. Because full exhaustive construction becomes computationally prohibitive for moderate-sized problems, we propose a filtering approach to prune the working set. Empirical results demonstrate that this filtering is effective at reducing computation while incurring only negligible reduction in quality. In summarizing our findings, we provide some characterization of the run-time vs quality trade-off involved.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge