Single-Step Consistent Diffusion Samplers

Sampling from unnormalized target distributions is a fundamental yet challenging task in machine learning and statistics. Existing sampling algorithms typically require many iterative steps to produce high-quality samples, leading to high computational costs that limit their practicality in time-sensitive or resource-constrained settings. In this work, we introduce consistent diffusion samplers, a new class of samplers designed to generate high-fidelity samples in a single step. We first develop a distillation algorithm to train a consistent diffusion sampler from a pretrained diffusion model without pre-collecting large datasets of samples. Our algorithm leverages incomplete sampling trajectories and noisy intermediate states directly from the diffusion process. We further propose a method to train a consistent diffusion sampler from scratch, fully amortizing exploration by training a single model that both performs diffusion sampling and skips intermediate steps using a self-consistency loss. Through extensive experiments on a variety of unnormalized distributions, we show that our approach yields high-fidelity samples using less than 1% of the network evaluations required by traditional diffusion samplers.

Controlled LLM Decoding via Discrete Auto-regressive Biasing

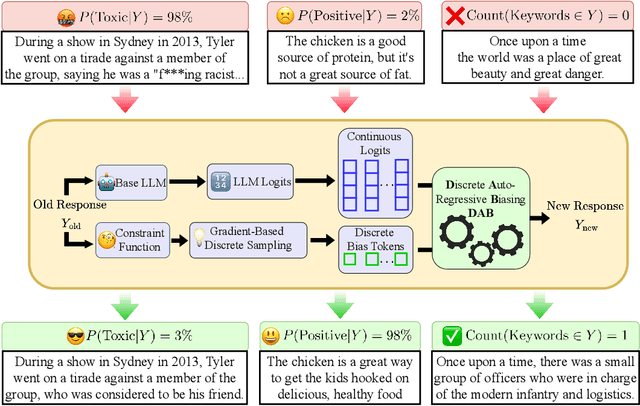
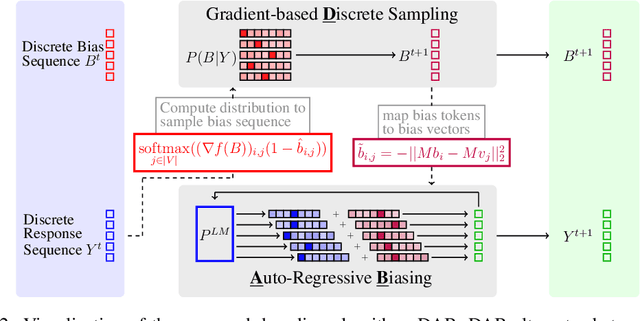
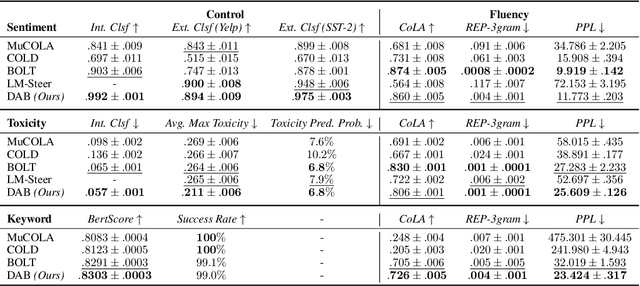
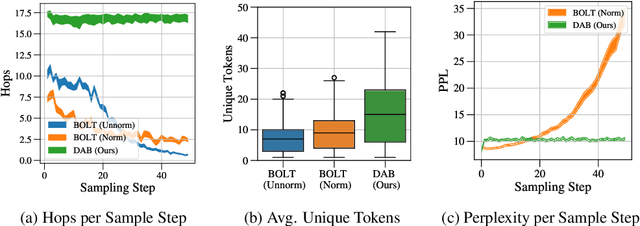
Controlled text generation allows for enforcing user-defined constraints on large language model outputs, an increasingly important field as LLMs become more prevalent in everyday life. One common approach uses energy-based decoding, which defines a target distribution through an energy function that combines multiple constraints into a weighted average. However, these methods often struggle to balance fluency with constraint satisfaction, even with extensive tuning of the energy function's coefficients. In this paper, we identify that this suboptimal balance arises from sampling in continuous space rather than the natural discrete space of text tokens. To address this, we propose Discrete Auto-regressive Biasing, a controlled decoding algorithm that leverages gradients while operating entirely in the discrete text domain. Specifically, we introduce a new formulation for controlled text generation by defining a joint distribution over the generated sequence and an auxiliary bias sequence. To efficiently sample from this joint distribution, we propose a Langevin-within-Gibbs sampling algorithm using gradient-based discrete MCMC. Our method significantly improves constraint satisfaction while maintaining comparable or better fluency, all with even lower computational costs. We demonstrate the advantages of our controlled decoding method on sentiment control, language detoxification, and keyword-guided generation.

Gradient-based Discrete Sampling with Automatic Cyclical Scheduling

Discrete distributions, particularly in high-dimensional deep models, are often highly multimodal due to inherent discontinuities. While gradient-based discrete sampling has proven effective, it is susceptible to becoming trapped in local modes due to the gradient information. To tackle this challenge, we propose an automatic cyclical scheduling, designed for efficient and accurate sampling in multimodal discrete distributions. Our method contains three key components: (1) a cyclical step size schedule where large steps discover new modes and small steps exploit each mode; (2) a cyclical balancing schedule, ensuring ``balanced" proposals for given step sizes and high efficiency of the Markov chain; and (3) an automatic tuning scheme for adjusting the hyperparameters in the cyclical schedules, allowing adaptability across diverse datasets with minimal tuning. We prove the non-asymptotic convergence and inference guarantee for our method in general discrete distributions. Extensive experiments demonstrate the superiority of our method in sampling complex multimodal discrete distributions.