Extracting Manifold Information from Point Clouds

A kernel based method is proposed for the construction of signature (defining) functions of subsets of $\mathbb{R}^d$. The subsets can range from full dimensional manifolds (open subsets) to point clouds (a finite number of points) and include bounded smooth manifolds of any codimension. The interpolation and analysis of point clouds are the main application. Two extreme cases in terms of regularity are considered, where the data set is interpolated by an analytic surface, at the one extreme, and by a H\"older continuous surface, at the other. The signature function can be computed as a linear combination of translated kernels, the coefficients of which are the solution of a finite dimensional linear problem. Once it is obtained, it can be used to estimate the dimension as well as the normal and the curvatures of the interpolated surface. The method is global and does not require explicit knowledge of local neighborhoods or any other structure present in the data set. It admits a variational formulation with a natural ``regularized'' counterpart, that proves to be useful in dealing with data sets corrupted by numerical error or noise. The underlying analytical structure of the approach is presented in general before it is applied to the case of point clouds.

Dimension Independent Data Sets Approximation and Applications to Classification

We revisit the classical kernel method of approximation/interpolation theory in a very specific context motivated by the desire to obtain a robust procedure to approximate discrete data sets by (super)level sets of functions that are merely continuous at the data set arguments but are otherwise smooth. Special functions, called data signals, are defined for any given data set and are used to succesfully solve supervised classification problems in a robust way that depends continuously on the data set. The efficacy of the method is illustrated with a series of low dimensional examples and by its application to the standard benchmark high dimensional problem of MNIST digit classification.

Improving LBP and its variants using anisotropic diffusion

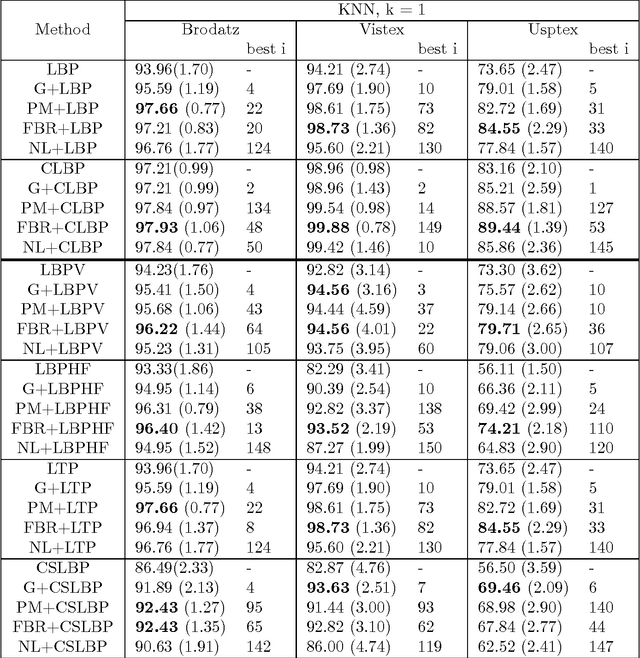
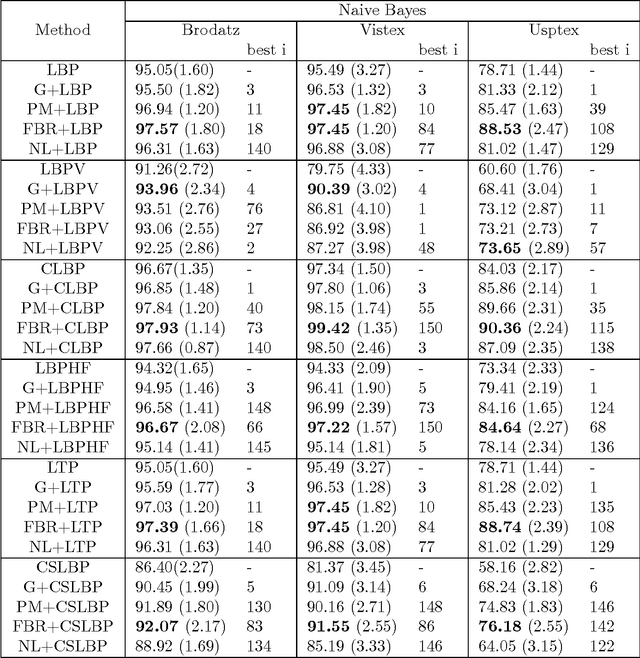
The main purpose of this paper is to propose a new preprocessing step in order to improve local feature descriptors and texture classification. Preprocessing is implemented by using transformations which help highlight salient features that play a significant role in texture recognition. We evaluate and compare four different competing methods: three different anisotropic diffusion methods including the classical anisotropic Perona-Malik diffusion and two subsequent regularizations of it and the application of a Gaussian kernel, which is the classical multiscale approach in texture analysis. The combination of the transformed images and the original ones are analyzed. The results show that the use of the preprocessing step does lead to improved texture recognition.