Extracting Manifold Information from Point Clouds

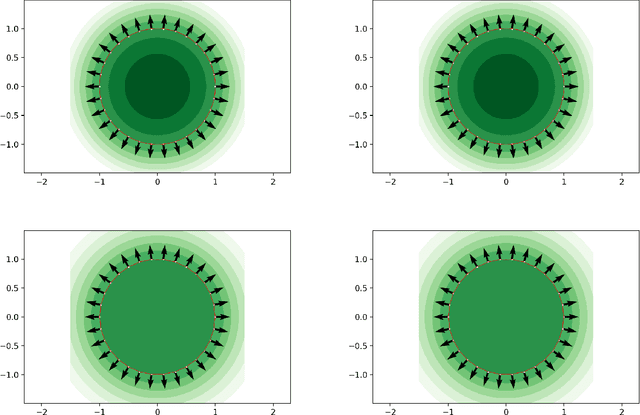
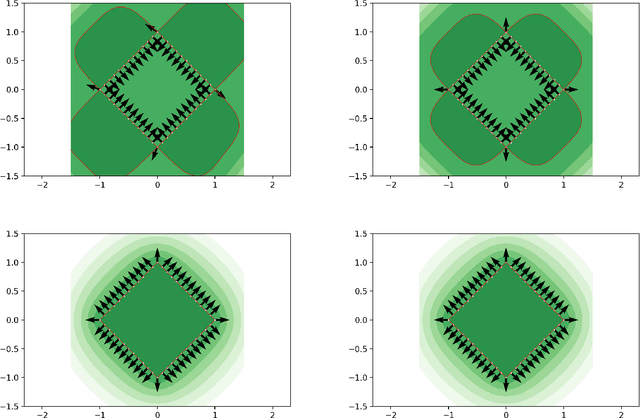
A kernel based method is proposed for the construction of signature (defining) functions of subsets of $\mathbb{R}^d$. The subsets can range from full dimensional manifolds (open subsets) to point clouds (a finite number of points) and include bounded smooth manifolds of any codimension. The interpolation and analysis of point clouds are the main application. Two extreme cases in terms of regularity are considered, where the data set is interpolated by an analytic surface, at the one extreme, and by a H\"older continuous surface, at the other. The signature function can be computed as a linear combination of translated kernels, the coefficients of which are the solution of a finite dimensional linear problem. Once it is obtained, it can be used to estimate the dimension as well as the normal and the curvatures of the interpolated surface. The method is global and does not require explicit knowledge of local neighborhoods or any other structure present in the data set. It admits a variational formulation with a natural ``regularized'' counterpart, that proves to be useful in dealing with data sets corrupted by numerical error or noise. The underlying analytical structure of the approach is presented in general before it is applied to the case of point clouds.