Semi-supervised Learning of Pushforwards For Domain Translation & Adaptation

Given two probability densities on related data spaces, we seek a map pushing one density to the other while satisfying application-dependent constraints. For maps to have utility in a broad application space (including domain translation, domain adaptation, and generative modeling), the map must be available to apply on out-of-sample data points and should correspond to a probabilistic model over the two spaces. Unfortunately, existing approaches, which are primarily based on optimal transport, do not address these needs. In this paper, we introduce a novel pushforward map learning algorithm that utilizes normalizing flows to parameterize the map. We first re-formulate the classical optimal transport problem to be map-focused and propose a learning algorithm to select from all possible maps under the constraint that the map minimizes a probability distance and application-specific regularizers; thus, our method can be seen as solving a modified optimal transport problem. Once the map is learned, it can be used to map samples from a source domain to a target domain. In addition, because the map is parameterized as a composition of normalizing flows, it models the empirical distributions over the two data spaces and allows both sampling and likelihood evaluation for both data sets. We compare our method (parOT) to related optimal transport approaches in the context of domain adaptation and domain translation on benchmark data sets. Finally, to illustrate the impact of our work on applied problems, we apply parOT to a real scientific application: spectral calibration for high-dimensional measurements from two vastly different environments

Generative structured normalizing flow Gaussian processes applied to spectroscopic data

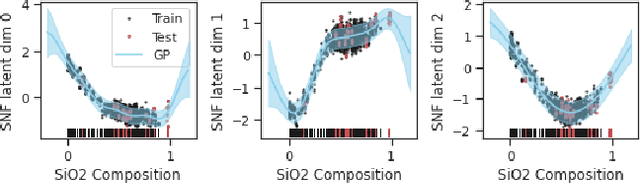
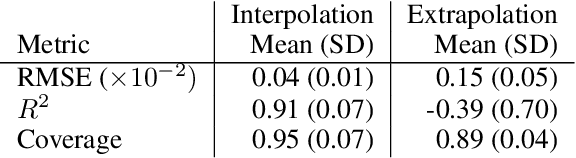
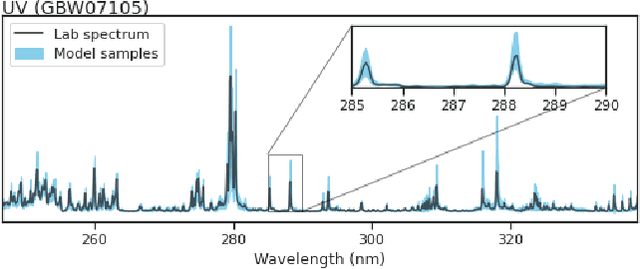
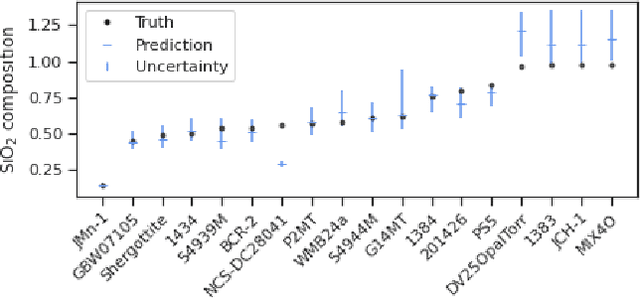
In this work, we propose a novel generative model for mapping inputs to structured, high-dimensional outputs using structured conditional normalizing flows and Gaussian process regression. The model is motivated by the need to characterize uncertainty in the input/output relationship when making inferences on new data. In particular, in the physical sciences, limited training data may not adequately characterize future observed data; it is critical that models adequately indicate uncertainty, particularly when they may be asked to extrapolate. In our proposed model, structured conditional normalizing flows provide parsimonious latent representations that relate to the inputs through a Gaussian process, providing exact likelihood calculations and uncertainty that naturally increases away from the training data inputs. We demonstrate the methodology on laser-induced breakdown spectroscopy data from the ChemCam instrument onboard the Mars rover Curiosity. ChemCam was designed to recover the chemical composition of rock and soil samples by measuring the spectral properties of plasma atomic emissions induced by a laser pulse. We show that our model can generate realistic spectra conditional on a given chemical composition and that we can use the model to perform uncertainty quantification of chemical compositions for new observed spectra. Based on our results, we anticipate that our proposed modeling approach may be useful in other scientific domains with high-dimensional, complex structure where it is important to quantify predictive uncertainty.