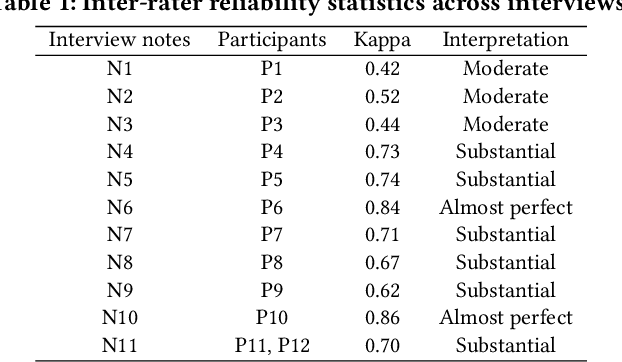
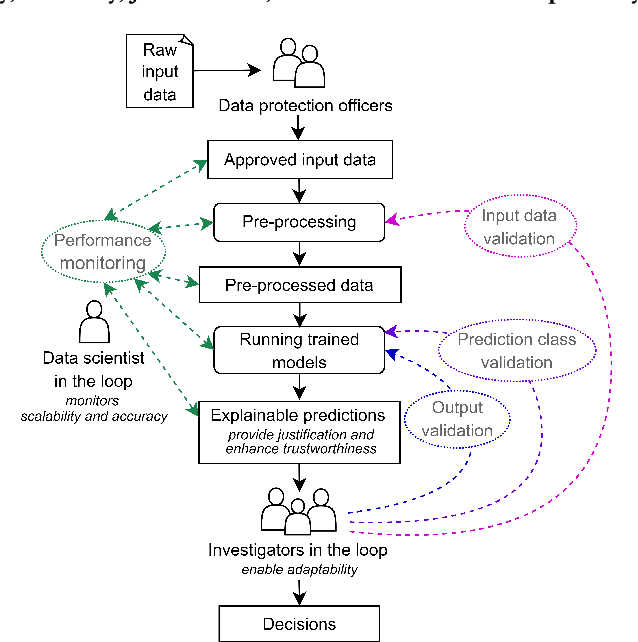
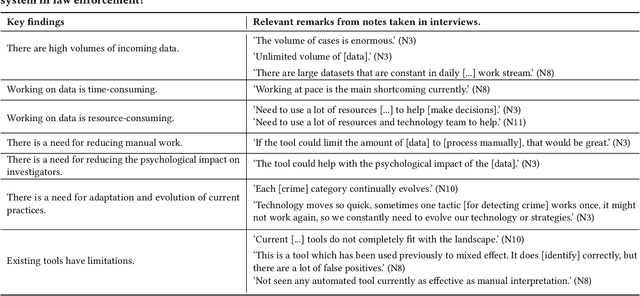
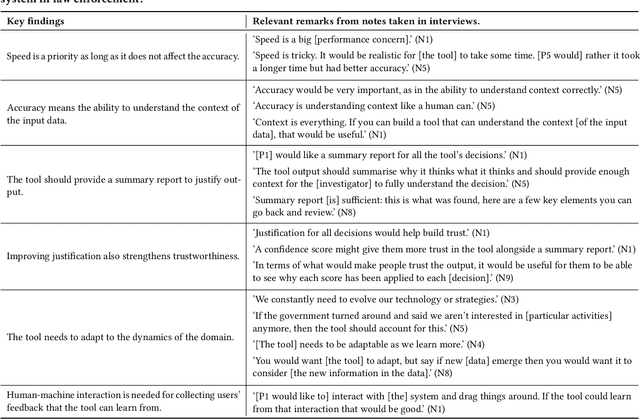
Towards User-Centred Design of AI-Assisted Decision-Making in Law Enforcement

Artificial Intelligence (AI) has become an important part of our everyday lives, yet user requirements for designing AI-assisted systems in law enforcement remain unclear. To address this gap, we conducted qualitative research on decision-making within a law enforcement agency. Our study aimed to identify limitations of existing practices, explore user requirements and understand the responsibilities that humans expect to undertake in these systems. Participants in our study highlighted the need for a system capable of processing and analysing large volumes of data efficiently to help in crime detection and prevention. Additionally, the system should satisfy requirements for scalability, accuracy, justification, trustworthiness and adaptability to be adopted in this domain. Participants also emphasised the importance of having end users review the input data that might be challenging for AI to interpret, and validate the generated output to ensure the system's accuracy. To keep up with the evolving nature of the law enforcement domain, end users need to help the system adapt to the changes in criminal behaviour and government guidance, and technical experts need to regularly oversee and monitor the system. Furthermore, user-friendly human interaction with the system is essential for its adoption and some of the participants confirmed they would be happy to be in the loop and provide necessary feedback that the system can learn from. Finally, we argue that it is very unlikely that the system will ever achieve full automation due to the dynamic and complex nature of the law enforcement domain.

Networked Communication for Mean-Field Games with Function Approximation and Empirical Mean-Field Estimation

Recent works have provided algorithms by which decentralised agents, which may be connected via a communication network, can learn equilibria in Mean-Field Games from a single, non-episodic run of the empirical system. However, these algorithms are given for tabular settings: this computationally limits the size of players' observation space, meaning that the algorithms are not able to handle anything but small state spaces, nor to generalise beyond policies depending on the ego player's state to so-called 'population-dependent' policies. We address this limitation by introducing function approximation to the existing setting, drawing on the Munchausen Online Mirror Descent method that has previously been employed only in finite-horizon, episodic, centralised settings. While this permits us to include the population's mean-field distribution in the observation for each player's policy, it is arguably unrealistic to assume that decentralised agents would have access to this global information: we therefore additionally provide new algorithms that allow agents to estimate the global empirical distribution based on a local neighbourhood, and to improve this estimate via communication over a given network. Our experiments showcase how the communication network allows decentralised agents to estimate the mean-field distribution for population-dependent policies, and that exchanging policy information helps networked agents to outperform both independent and even centralised agents in function-approximation settings, by an even greater margin than in tabular settings.

Networked Communication for Decentralised Agents in Mean-Field Games

We introduce networked communication to the mean-field game framework. In particular, we look at oracle-free settings where $N$ decentralised agents learn along a single, non-episodic evolution path of the empirical system, such as we may encounter for a large range of many-agent cooperation problems in the real-world. We provide theoretical evidence that by spreading improved policies through the network in a decentralised fashion, our sample guarantees are upper-bounded by those of the purely independent-learning case. Moreover, we show empirically that our networked method can give faster convergence in practice, while removing the reliance on a centralised controller. We also demonstrate that our decentralised communication architecture brings significant benefits over both the centralised and independent alternatives in terms of robustness and flexibility to unexpected learning failures and changes in population size. For comparison purposes with our new architecture, we modify recent algorithms for the centralised and independent cases to make their practical convergence feasible: while contributing the first empirical demonstrations of these algorithms in our setting of $N$ agents learning along a single system evolution with only local state observability, we additionally display the empirical benefits of our new, networked approach.