Get our free extension to see links to code for papers anywhere online!Free add-on: code for papers everywhere!Free add-on: See code for papers anywhere!
Pascal Tom Getreuer
Solving Image PDEs with a Shallow Network
Oct 15, 2021Figures and Tables: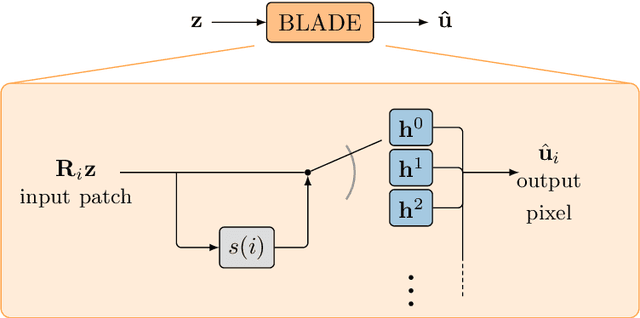
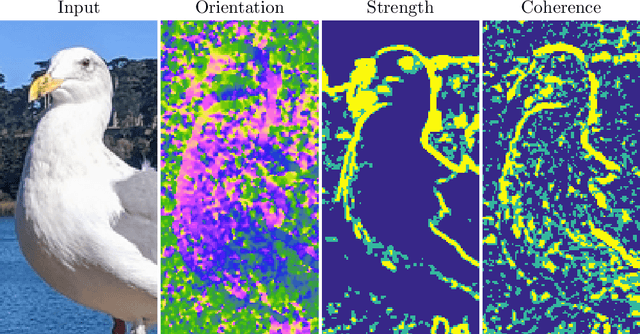
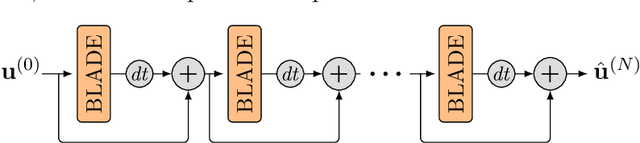
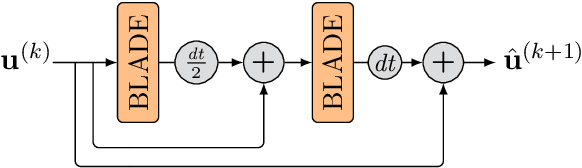




Abstract:Partial differential equations (PDEs) are typically used as models of physical processes but are also of great interest in PDE-based image processing. However, when it comes to their use in imaging, conventional numerical methods for solving PDEs tend to require very fine grid resolution for stability, and as a result have impractically high computational cost. This work applies BLADE (Best Linear Adaptive Enhancement), a shallow learnable filtering framework, to PDE solving, and shows that the resulting approach is efficient and accurate, operating more reliably at coarse grid resolutions than classical methods. As such, the model can be flexibly used for a wide variety of problems in imaging.
* 21 pages, 22 figures, references arXiv:1802.06130, arXiv:1711.10700,
arXiv:1606.01299
Via
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge