Picture for Pascal Castellazzi

Pascal Castellazzi

$k$-means on Positive Definite Matrices, and an Application to Clustering in Radar Image Sequences

Add code
Aug 26, 2020
Daniel Fryer, Hien Nguyen, Pascal Castellazzi
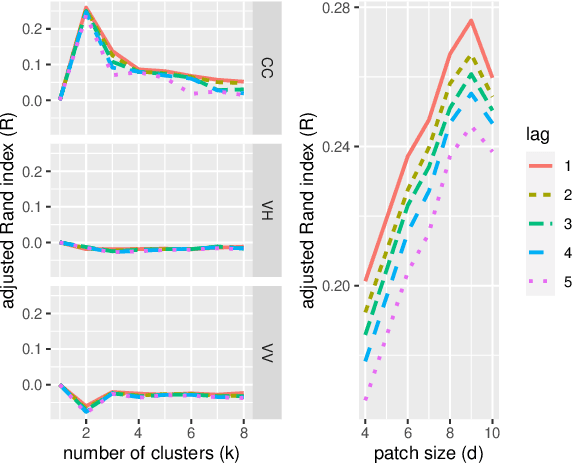
Figure 1 for $k$-means on Positive Definite Matrices, and an Application to Clustering in Radar Image Sequences
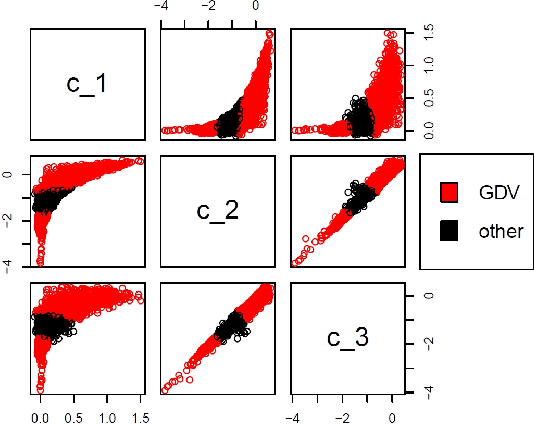
Figure 2 for $k$-means on Positive Definite Matrices, and an Application to Clustering in Radar Image Sequences
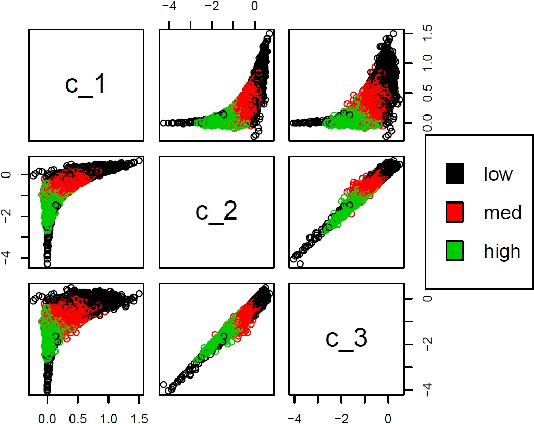
Figure 3 for $k$-means on Positive Definite Matrices, and an Application to Clustering in Radar Image Sequences
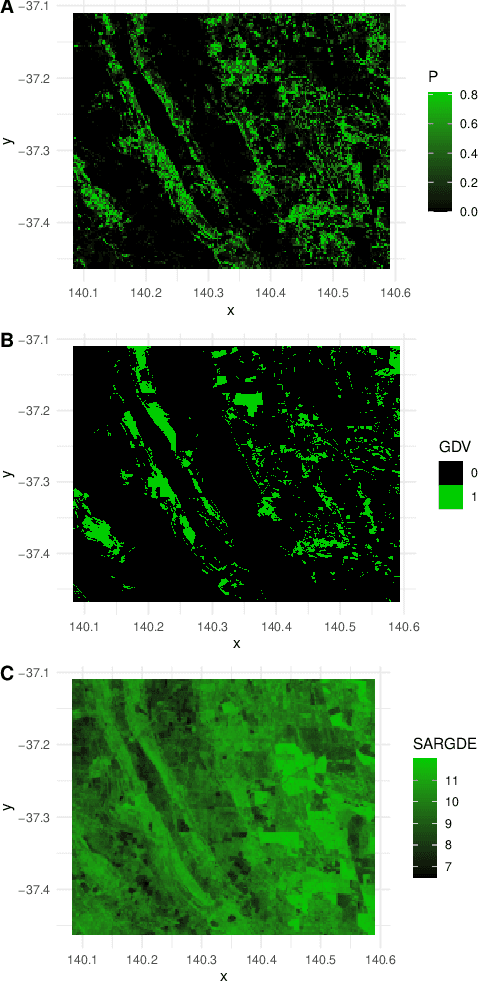
Figure 4 for $k$-means on Positive Definite Matrices, and an Application to Clustering in Radar Image Sequences

We state theoretical properties for $k$-means clustering of Symmetric Positive Definite (SPD) matrices, in a non-Euclidean space, that provides a natural and favourable representation of these data. We then provide a novel application for this method, to time-series clustering of pixels in a sequence of Synthetic Aperture Radar images, via their finite-lag autocovariance matrices.

* This work has been submitted to the IEEE for possible publication. Copyright may be transferred without notice, after which this version may no longer be accessible 
Viaarxiv icon
Github IconAccess Paper or Ask Questions
Twitter IconFacebook IconLinkedin IconWhatsapp IconMessenger Icon