Shapley values for feature selection: The good, the bad, and the axioms

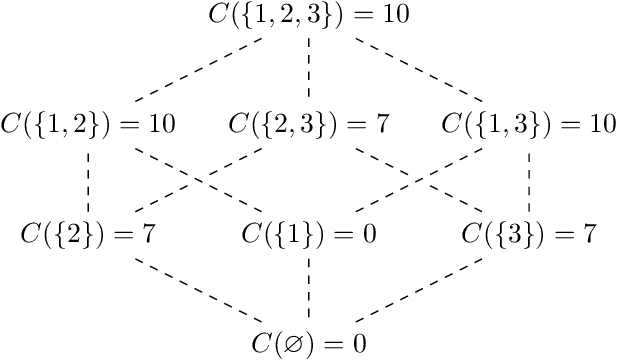
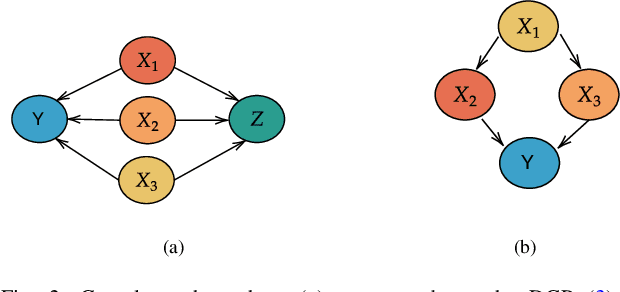
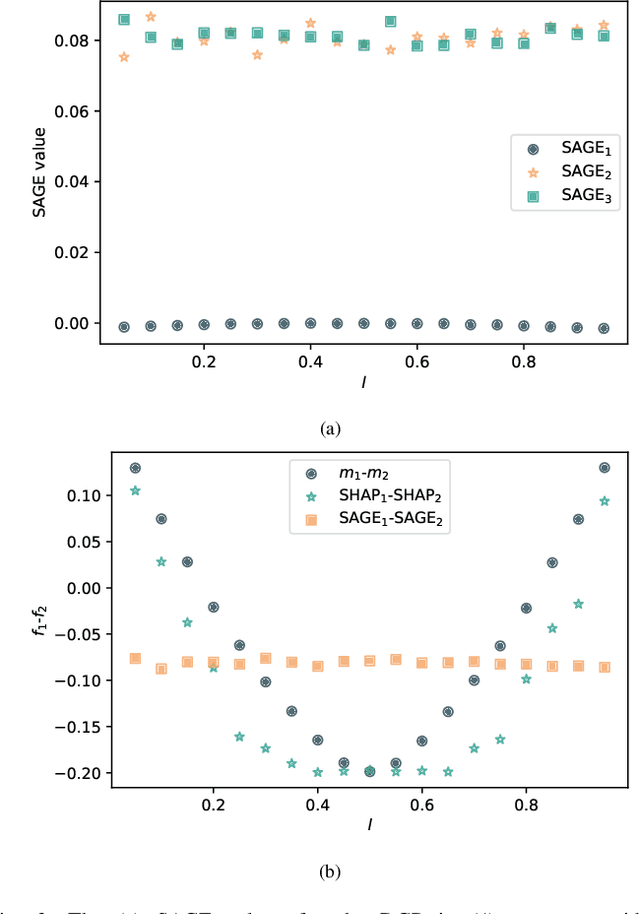
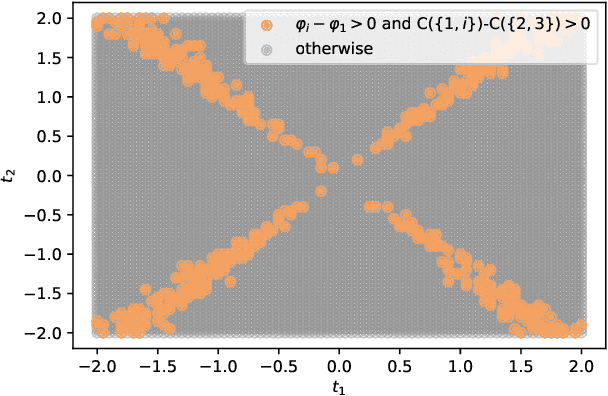
The Shapley value has become popular in the Explainable AI (XAI) literature, thanks, to a large extent, to a solid theoretical foundation, including four "favourable and fair" axioms for attribution in transferable utility games. The Shapley value is provably the only solution concept satisfying these axioms. In this paper, we introduce the Shapley value and draw attention to its recent uses as a feature selection tool. We call into question this use of the Shapley value, using simple, abstract "toy" counterexamples to illustrate that the axioms may work against the goals of feature selection. From this, we develop a number of insights that are then investigated in concrete simulation settings, with a variety of Shapley value formulations, including SHapley Additive exPlanations (SHAP) and Shapley Additive Global importancE (SAGE).

$k$-means on Positive Definite Matrices, and an Application to Clustering in Radar Image Sequences

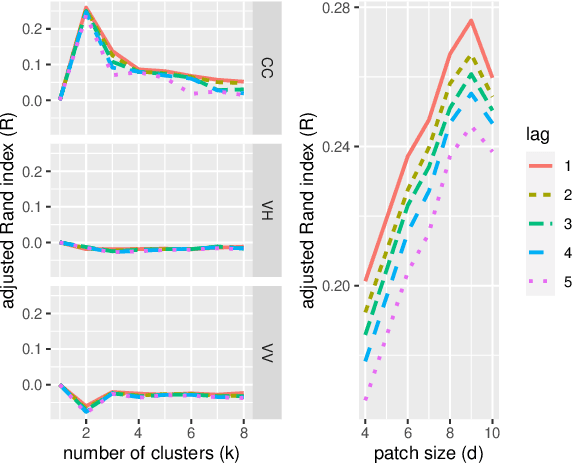
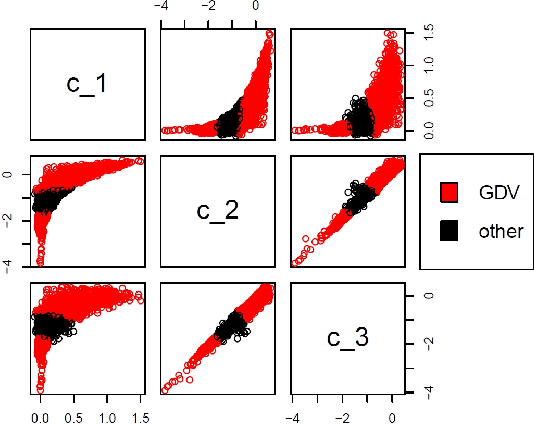
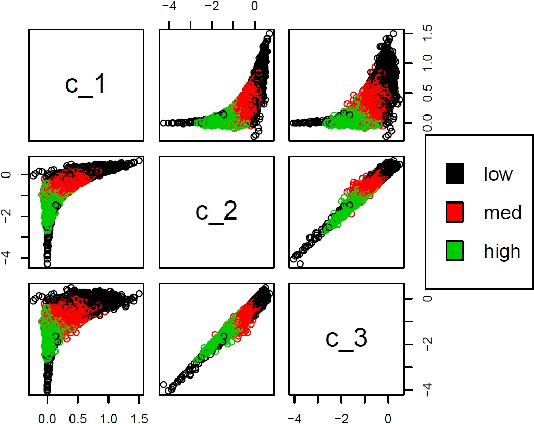
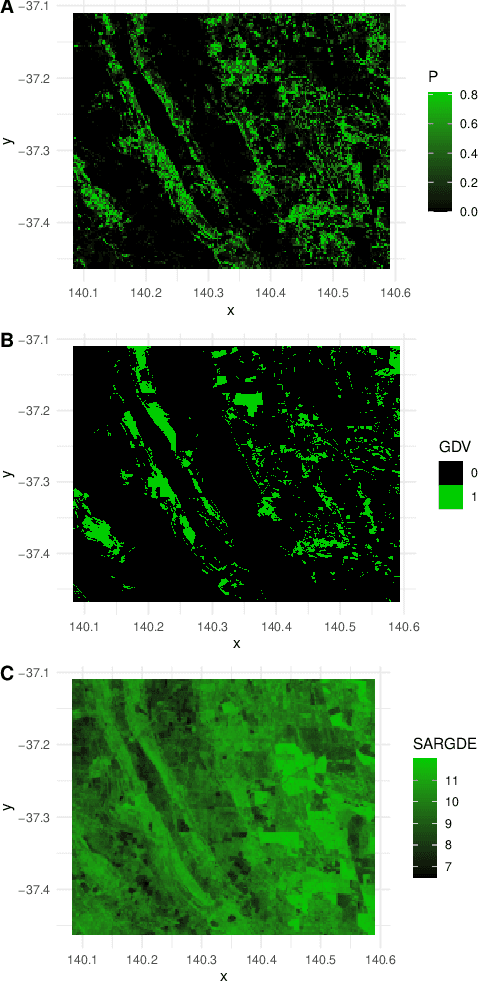
We state theoretical properties for $k$-means clustering of Symmetric Positive Definite (SPD) matrices, in a non-Euclidean space, that provides a natural and favourable representation of these data. We then provide a novel application for this method, to time-series clustering of pixels in a sequence of Synthetic Aperture Radar images, via their finite-lag autocovariance matrices.