Trend Detection based Regret Minimization for Bandit Problems

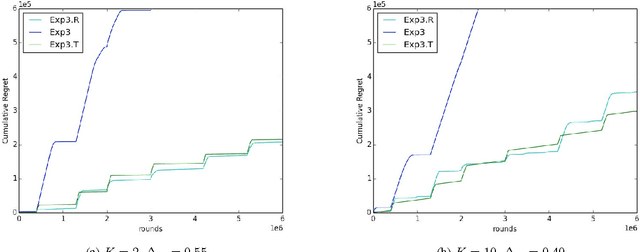
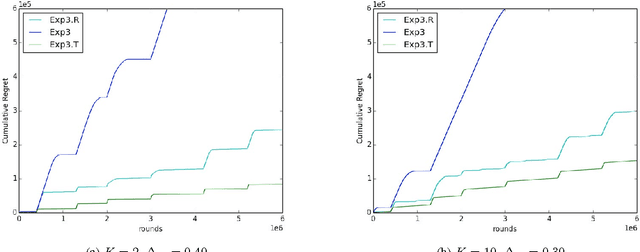
We study a variation of the classical multi-armed bandits problem. In this problem, the learner has to make a sequence of decisions, picking from a fixed set of choices. In each round, she receives as feedback only the loss incurred from the chosen action. Conventionally, this problem has been studied when losses of the actions are drawn from an unknown distribution or when they are adversarial. In this paper, we study this problem when the losses of the actions also satisfy certain structural properties, and especially, do show a trend structure. When this is true, we show that using \textit{trend detection}, we can achieve regret of order $\tilde{O} (N \sqrt{TK})$ with respect to a switching strategy for the version of the problem where a single action is chosen in each round and $\tilde{O} (Nm \sqrt{TK})$ when $m$ actions are chosen each round. This guarantee is a significant improvement over the conventional benchmark. Our approach can, as a framework, be applied in combination with various well-known bandit algorithms, like Exp3. For both versions of the problem, we give regret guarantees also for the \textit{anytime} setting, i.e. when the length of the choice-sequence is not known in advance. Finally, we pinpoint the advantages of our method by comparing it to some well-known other strategies.

Dynamic Pricing in Competitive Markets

Dynamic pricing of goods in a competitive environment to maximize revenue is a natural objective and has been a subject of research over the years. In this paper, we focus on a class of markets exhibiting the substitutes property with sellers having divisible and replenishable goods. Depending on the prices chosen, each seller observes a certain demand which is satisfied subject to the supply constraint. The goal of the seller is to price her good dynamically so as to maximize her revenue. For the static market case, when the consumer utility satisfies the Constant Elasticity of Substitution (CES) property, we give a $O(\sqrt{T})$ regret bound on the maximum loss in revenue of a seller using a modified version of the celebrated Online Gradient Descent Algorithm by Zinkevich. For a more specialized set of consumer utilities satisfying the iso-elasticity condition, we show that when each seller uses a regret-minimizing algorithm satisfying a certain technical property, the regret with respect to $(1-\alpha)$ times optimal revenue is bounded as $O(T^{1/4} / \sqrt{\alpha})$. We extend this result to markets with dynamic supplies and prove a corresponding dynamic regret bound, whose guarantee deteriorates smoothly with the inherent instability of the market. As a side-result, we also extend the previously known convergence results of these algorithms in a general game to the dynamic setting.