Trend Detection based Regret Minimization for Bandit Problems
Paper and Code
Sep 15, 2017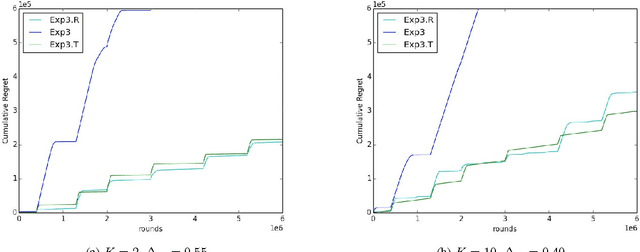
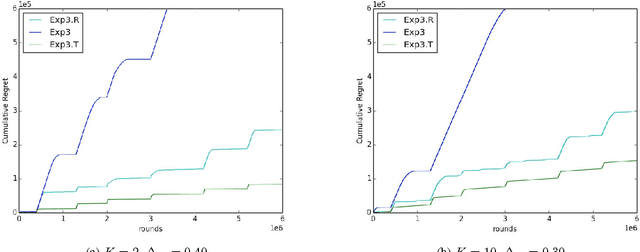
We study a variation of the classical multi-armed bandits problem. In this problem, the learner has to make a sequence of decisions, picking from a fixed set of choices. In each round, she receives as feedback only the loss incurred from the chosen action. Conventionally, this problem has been studied when losses of the actions are drawn from an unknown distribution or when they are adversarial. In this paper, we study this problem when the losses of the actions also satisfy certain structural properties, and especially, do show a trend structure. When this is true, we show that using \textit{trend detection}, we can achieve regret of order $\tilde{O} (N \sqrt{TK})$ with respect to a switching strategy for the version of the problem where a single action is chosen in each round and $\tilde{O} (Nm \sqrt{TK})$ when $m$ actions are chosen each round. This guarantee is a significant improvement over the conventional benchmark. Our approach can, as a framework, be applied in combination with various well-known bandit algorithms, like Exp3. For both versions of the problem, we give regret guarantees also for the \textit{anytime} setting, i.e. when the length of the choice-sequence is not known in advance. Finally, we pinpoint the advantages of our method by comparing it to some well-known other strategies.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge