The Role of Fibration Symmetries in Geometric Deep Learning

Geometric Deep Learning (GDL) unifies a broad class of machine learning techniques from the perspectives of symmetries, offering a framework for introducing problem-specific inductive biases like Graph Neural Networks (GNNs). However, the current formulation of GDL is limited to global symmetries that are not often found in real-world problems. We propose to relax GDL to allow for local symmetries, specifically fibration symmetries in graphs, to leverage regularities of realistic instances. We show that GNNs apply the inductive bias of fibration symmetries and derive a tighter upper bound for their expressive power. Additionally, by identifying symmetries in networks, we collapse network nodes, thereby increasing their computational efficiency during both inference and training of deep neural networks. The mathematical extension introduced here applies beyond graphs to manifolds, bundles, and grids for the development of models with inductive biases induced by local symmetries that can lead to better generalization.

Monotonicity in Undirected Networks

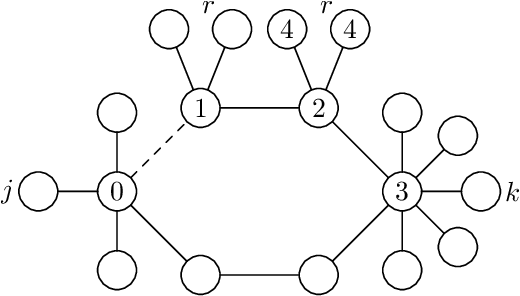
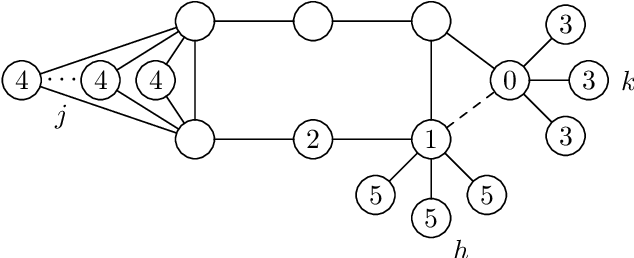
Is it always beneficial to create a new relationship (have a new follower/friend) in a social network? This question can be formally stated as a property of the centrality measure that defines the importance of the actors of the network. Score monotonicity means that adding an arc increases the centrality score of the target of the arc; rank monotonicity means that adding an arc improves the importance of the target of the arc relatively to the remaining nodes. It is known that most centralities are both score and rank monotone on directed, strongly connected graphs. In this paper, we study the problem of score and rank monotonicity for classical centrality measures in the case of undirected networks: in this case, we require that score, or relative importance, improve at both endpoints of the new edge. We show that, surprisingly, the situation in the undirected case is very different, and in particular that closeness, harmonic centrality, betweenness, eigenvector centrality, Seeley's index, Katz's index, and PageRank are not rank monotone; betweenness and PageRank are not even score monotone. In other words, while it is always a good thing to get a new follower, it is not always beneficial to get a new friend.

Spectral Rank Monotonicity on Undirected Networks

We study the problem of score and rank monotonicity for spectral ranking methods, such as eigenvector centrality and PageRank, in the case of undirected networks. Score monotonicity means that adding an edge increases the score at both ends of the edge. Rank monotonicity means that adding an edge improves the relative position of both ends of the edge with respect to the remaining nodes. It is known that common spectral rankings are both score and rank monotone on directed, strongly connected graphs. We show that, surprisingly, the situation is very different for undirected graphs, and in particular that PageRank is neither score nor rank monotone.

Estimating latent feature-feature interactions in large feature-rich graphs

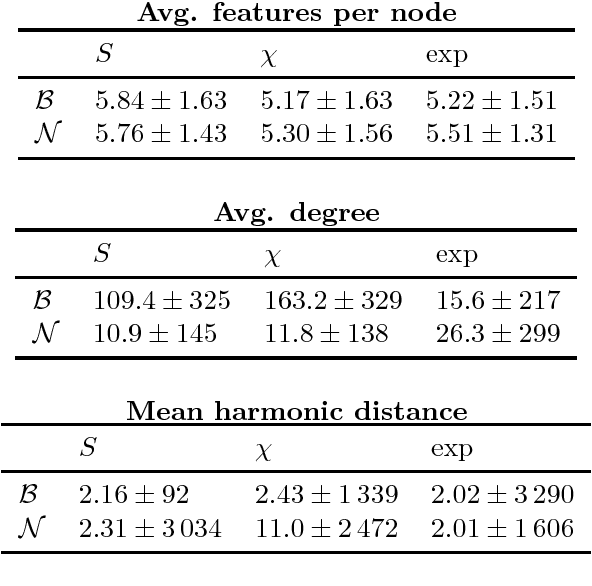
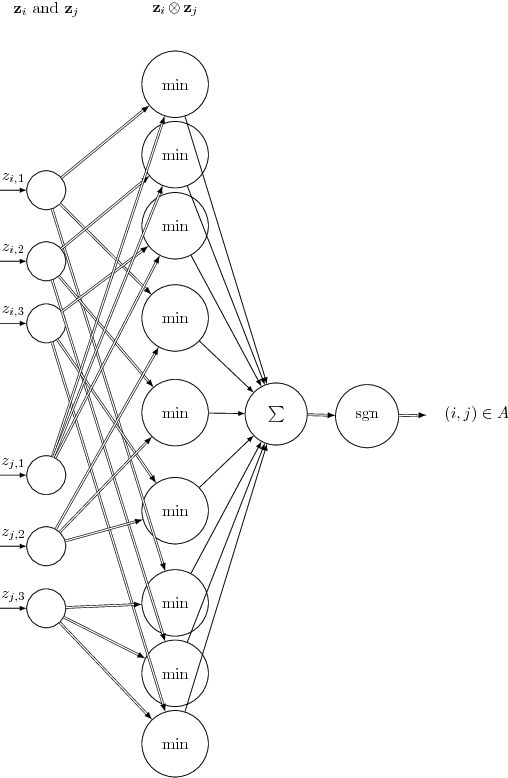
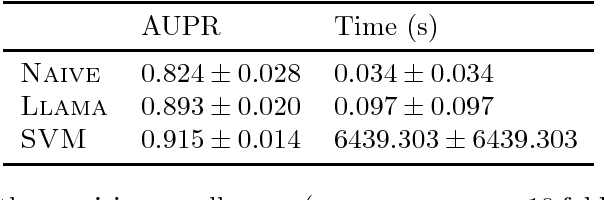
Real-world complex networks describe connections between objects; in reality, those objects are often endowed with some kind of features. How does the presence or absence of such features interplay with the network link structure? Although the situation here described is truly ubiquitous, there is a limited body of research dealing with large graphs of this kind. Many previous works considered homophily as the only possible transmission mechanism translating node features into links. Other authors, instead, developed more sophisticated models, that are able to handle complex feature interactions, but are unfit to scale to very large networks. We expand on the MGJ model, where interactions between pairs of features can foster or discourage link formation. In this work, we will investigate how to estimate the latent feature-feature interactions in this model. We shall propose two solutions: the first one assumes feature independence and it is essentially based on Naive Bayes; the second one, which relaxes the independence assumption assumption, is based on perceptrons. In fact, we show it is possible to cast the model equation in order to see it as the prediction rule of a perceptron. We analyze how classical results for the perceptrons can be interpreted in this context; then, we define a fast and simple perceptron-like algorithm for this task, which can process $10^8$ links in minutes. We then compare these two techniques, first with synthetic datasets that follows our model, gaining evidence that the Naive independence assumptions are detrimental in practice. Secondly, we consider a real, large-scale citation network where each node (i.e., paper) can be described by different types of characteristics; there, our algorithm can assess how well each set of features can explain the links, and thus finding meaningful latent feature-feature interactions.