Bandit-Based Policy Invariant Explicit Shaping for Incorporating External Advice in Reinforcement Learning

A key challenge for a reinforcement learning (RL) agent is to incorporate external/expert1 advice in its learning. The desired goals of an algorithm that can shape the learning of an RL agent with external advice include (a) maintaining policy invariance; (b) accelerating the learning of the agent; and (c) learning from arbitrary advice [3]. To address this challenge this paper formulates the problem of incorporating external advice in RL as a multi-armed bandit called shaping-bandits. The reward of each arm of shaping bandits corresponds to the return obtained by following the expert or by following a default RL algorithm learning on the true environment reward.We show that directly applying existing bandit and shaping algorithms that do not reason about the non-stationary nature of the underlying returns can lead to poor results. Thus we propose UCB-PIES (UPIES), Racing-PIES (RPIES), and Lazy PIES (LPIES) three different shaping algorithms built on different assumptions that reason about the long-term consequences of following the expert policy or the default RL algorithm. Our experiments in four different settings show that these proposed algorithms achieve the above-mentioned goals whereas the other algorithms fail to do so.

Useful Policy Invariant Shaping from Arbitrary Advice

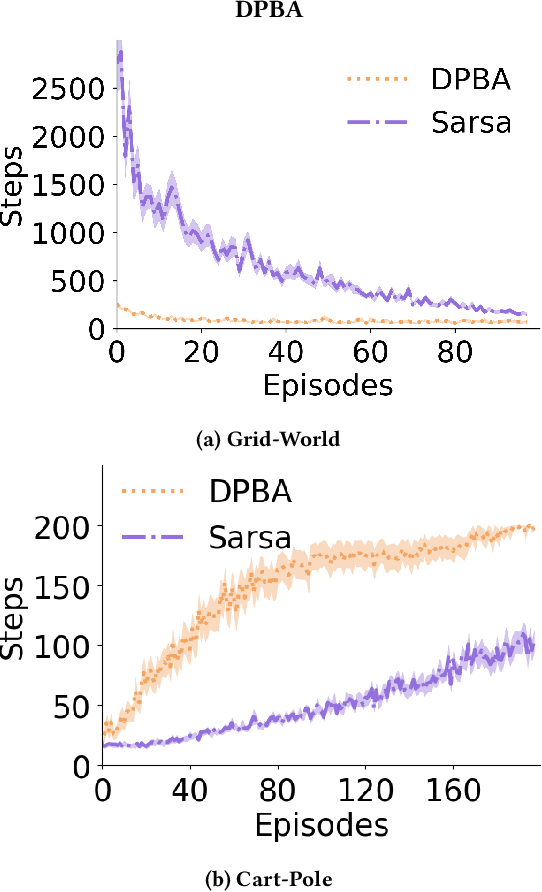
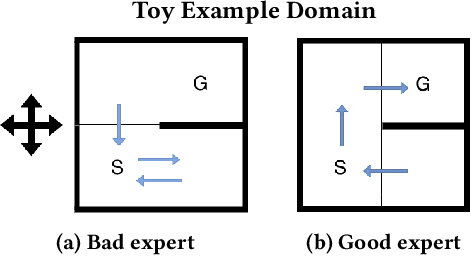
Reinforcement learning is a powerful learning paradigm in which agents can learn to maximize sparse and delayed reward signals. Although RL has had many impressive successes in complex domains, learning can take hours, days, or even years of training data. A major challenge of contemporary RL research is to discover how to learn with less data. Previous work has shown that domain information can be successfully used to shape the reward; by adding additional reward information, the agent can learn with much less data. Furthermore, if the reward is constructed from a potential function, the optimal policy is guaranteed to be unaltered. While such potential-based reward shaping (PBRS) holds promise, it is limited by the need for a well-defined potential function. Ideally, we would like to be able to take arbitrary advice from a human or other agent and improve performance without affecting the optimal policy. The recently introduced dynamic potential based advice (DPBA) method tackles this challenge by admitting arbitrary advice from a human or other agent and improves performance without affecting the optimal policy. The main contribution of this paper is to expose, theoretically and empirically, a flaw in DPBA. Alternatively, to achieve the ideal goals, we present a simple method called policy invariant explicit shaping (PIES) and show theoretically and empirically that PIES succeeds where DPBA fails.