Deep learning-driven scheduling algorithm for a single machine problem minimizing the total tardiness

In this paper, we investigate the use of the deep learning method for solving a well-known NP-hard single machine scheduling problem with the objective of minimizing the total tardiness. We propose a deep neural network that acts as a polynomial-time estimator of the criterion value used in a single-pass scheduling algorithm based on Lawler's decomposition and symmetric decomposition proposed by Della Croce et al. Essentially, the neural network guides the algorithm by estimating the best splitting of the problem into subproblems. The paper also describes a new method for generating the training data set, which speeds up the training dataset generation and reduces the average optimality gap of solutions. The experimental results show that our machine learning-driven approach can efficiently generalize information from the training phase to significantly larger instances. Even though the instances used in the training phase have from 75 to 100 jobs, the average optimality gap on instances with up to 800 jobs is 0.26%, which is almost five times less than the gap of the state-of-the-art heuristic.

Data-driven Algorithm for Scheduling with Total Tardiness

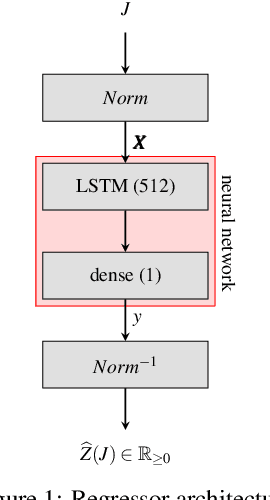
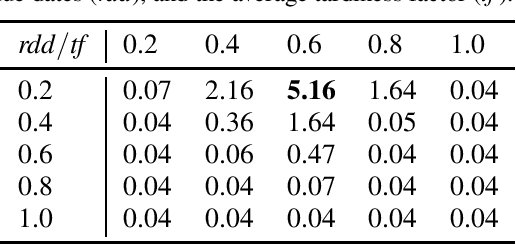
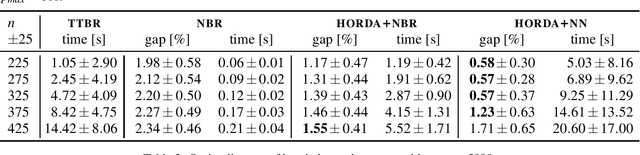
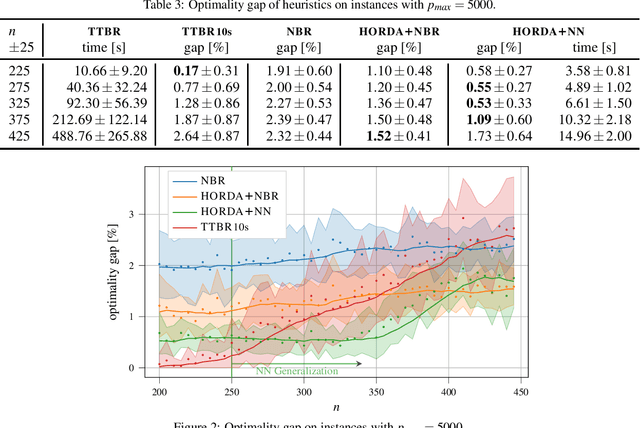
In this paper, we investigate the use of deep learning for solving a classical NP-Hard single machine scheduling problem where the criterion is to minimize the total tardiness. Instead of designing an end-to-end machine learning model, we utilize well known decomposition of the problem and we enhance it with a data-driven approach. We have designed a regressor containing a deep neural network that learns and predicts the criterion of a given set of jobs. The network acts as a polynomial-time estimator of the criterion that is used in a single-pass scheduling algorithm based on Lawler's decomposition theorem. Essentially, the regressor guides the algorithm to select the best position for each job. The experimental results show that our data-driven approach can efficiently generalize information from the training phase to significantly larger instances (up to 350 jobs) where it achieves an optimality gap of about 0.5%, which is four times less than the gap of the state-of-the-art NBR heuristic.

Roster Evaluation Based on Classifiers for the Nurse Rostering Problem

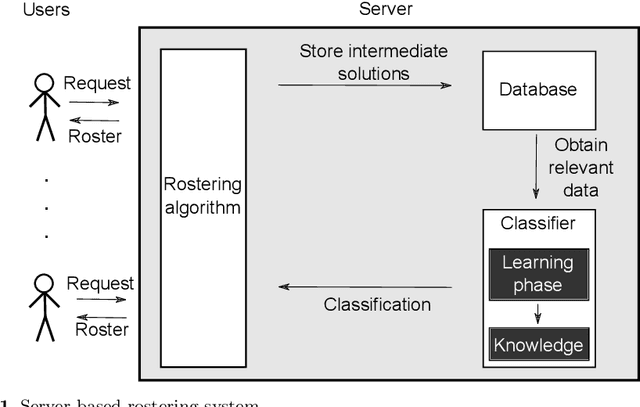
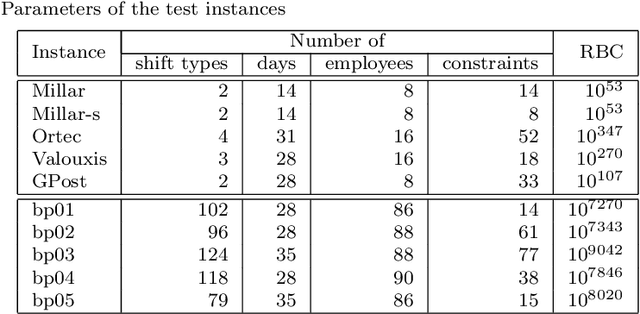
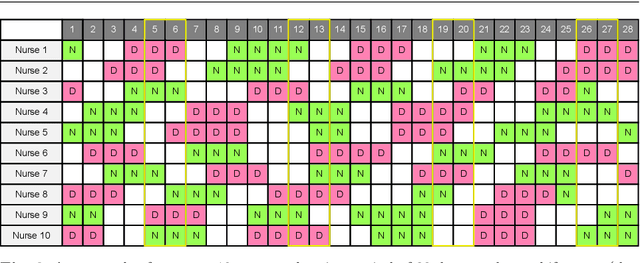
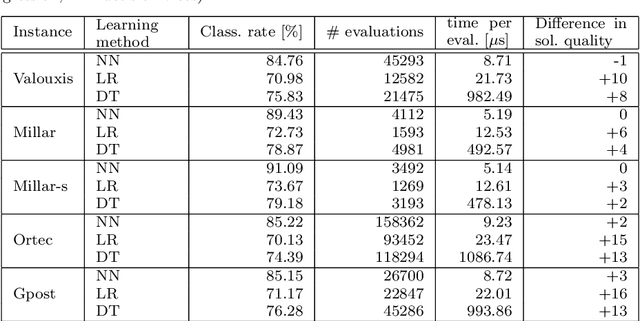
The personnel scheduling problem is a well-known NP-hard combinatorial problem. Due to the complexity of this problem and the size of the real-world instances, it is not possible to use exact methods, and thus heuristics, meta-heuristics, or hyper-heuristics must be employed. The majority of heuristic approaches are based on iterative search, where the quality of intermediate solutions must be calculated. Unfortunately, this is computationally highly expensive because these problems have many constraints and some are very complex. In this study, we propose a machine learning technique as a tool to accelerate the evaluation phase in heuristic approaches. The solution is based on a simple classifier, which is able to determine whether the changed solution (more precisely, the changed part of the solution) is better than the original or not. This decision is made much faster than a standard cost-oriented evaluation process. However, the classification process cannot guarantee 100% correctness. Therefore, our approach, which is illustrated using a tabu search algorithm in this study, includes a filtering mechanism, where the classifier rejects the majority of the potentially bad solutions and the remaining solutions are then evaluated in a standard manner. We also show how the boosting algorithms can improve the quality of the final solution compared with a simple classifier. We verified our proposed approach and premises, based on standard and real-world benchmark instances, to demonstrate the significant speedup obtained with comparable solution quality.

Energy Optimization of Robotic Cells

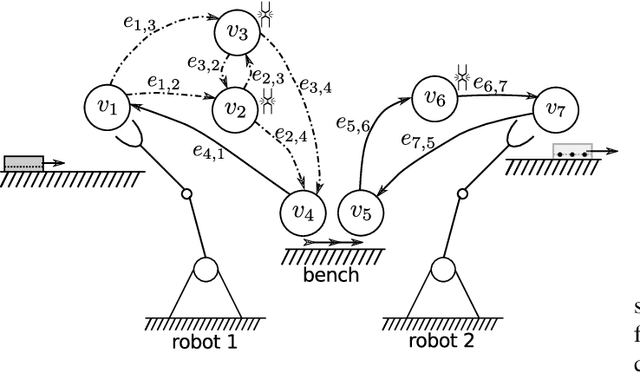
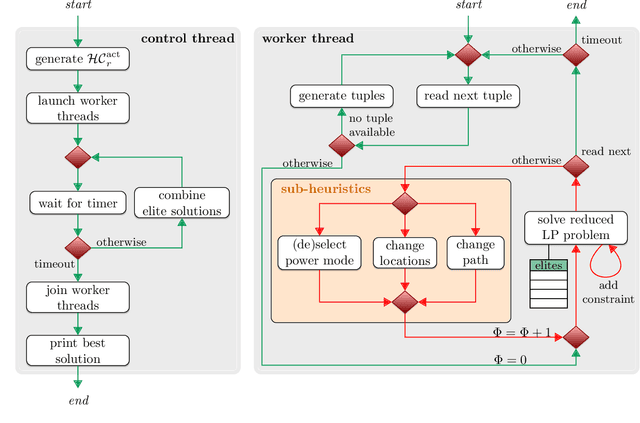
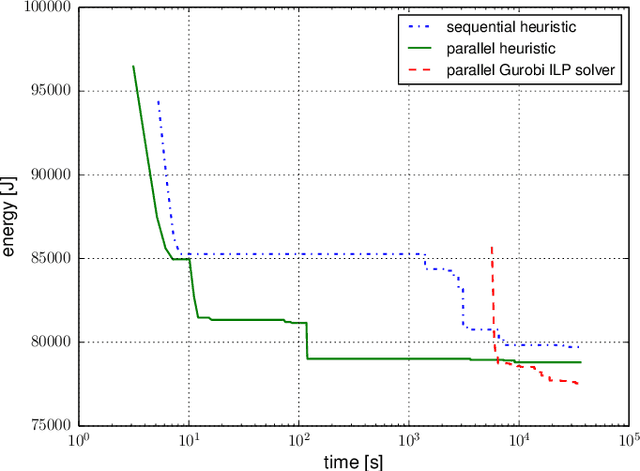
This study focuses on the energy optimization of industrial robotic cells, which is essential for sustainable production in the long term. A holistic approach that considers a robotic cell as a whole toward minimizing energy consumption is proposed. The mathematical model, which takes into account various robot speeds, positions, power-saving modes, and alternative orders of operations, can be transformed into a mixed-integer linear programming formulation that is, however, suitable only for small instances. To optimize complex robotic cells, a hybrid heuristic accelerated by using multicore processors and the Gurobi simplex method for piecewise linear convex functions is implemented. The experimental results showed that the heuristic solved 93 % of instances with a solution quality close to a proven lower bound. Moreover, compared with the existing works, which typically address problems with three to four robots, this study solved real-size problem instances with up to 12 robots and considered more optimization aspects. The proposed algorithms were also applied on an existing robotic cell in \v{S}koda Auto. The outcomes, based on simulations and measurements, indicate that, compared with the previous state (at maximal robot speeds and without deeper power-saving modes), the energy consumption can be reduced by about 20 % merely by optimizing the robot speeds and applying power-saving modes. All the software and generated datasets used in this research are publicly available.