Bottleneck Identification in Resource-Constrained Project Scheduling via Constraint Relaxation

In realistic production scenarios, Advanced Planning and Scheduling (APS) tools often require manual intervention by production planners, as the system works with incomplete information, resulting in suboptimal schedules. Often, the preferable solution is not found just because of the too-restrictive constraints specifying the optimization problem, representing bottlenecks in the schedule. To provide computer-assisted support for decision-making, we aim to automatically identify bottlenecks in the given schedule while linking them to the particular constraints to be relaxed. In this work, we address the problem of reducing the tardiness of a particular project in an obtained schedule in the resource-constrained project scheduling problem by relaxing constraints related to identified bottlenecks. We develop two methods for this purpose. The first method adapts existing approaches from the job shop literature and utilizes them for so-called untargeted relaxations. The second method identifies potential improvements in relaxed versions of the problem and proposes targeted relaxations. Surprisingly, the untargeted relaxations result in improvements comparable to the targeted relaxations.

Deep learning-driven scheduling algorithm for a single machine problem minimizing the total tardiness

In this paper, we investigate the use of the deep learning method for solving a well-known NP-hard single machine scheduling problem with the objective of minimizing the total tardiness. We propose a deep neural network that acts as a polynomial-time estimator of the criterion value used in a single-pass scheduling algorithm based on Lawler's decomposition and symmetric decomposition proposed by Della Croce et al. Essentially, the neural network guides the algorithm by estimating the best splitting of the problem into subproblems. The paper also describes a new method for generating the training data set, which speeds up the training dataset generation and reduces the average optimality gap of solutions. The experimental results show that our machine learning-driven approach can efficiently generalize information from the training phase to significantly larger instances. Even though the instances used in the training phase have from 75 to 100 jobs, the average optimality gap on instances with up to 800 jobs is 0.26%, which is almost five times less than the gap of the state-of-the-art heuristic.

Data-driven Algorithm for Scheduling with Total Tardiness

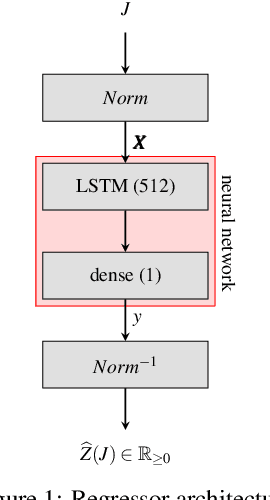
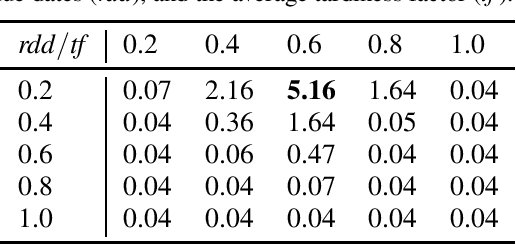
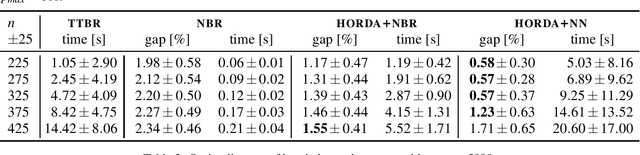
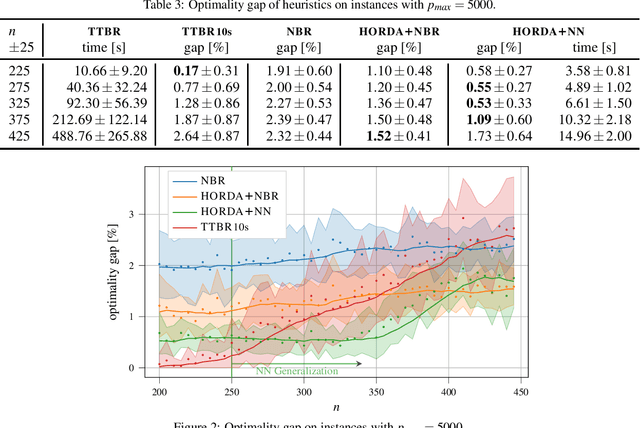
In this paper, we investigate the use of deep learning for solving a classical NP-Hard single machine scheduling problem where the criterion is to minimize the total tardiness. Instead of designing an end-to-end machine learning model, we utilize well known decomposition of the problem and we enhance it with a data-driven approach. We have designed a regressor containing a deep neural network that learns and predicts the criterion of a given set of jobs. The network acts as a polynomial-time estimator of the criterion that is used in a single-pass scheduling algorithm based on Lawler's decomposition theorem. Essentially, the regressor guides the algorithm to select the best position for each job. The experimental results show that our data-driven approach can efficiently generalize information from the training phase to significantly larger instances (up to 350 jobs) where it achieves an optimality gap of about 0.5%, which is four times less than the gap of the state-of-the-art NBR heuristic.