Removing Manually-Generated Boilerplate from Electronic Texts: Experiments with Project Gutenberg e-Books

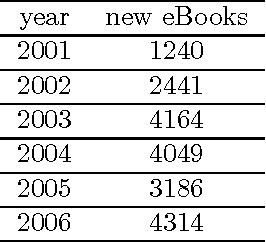
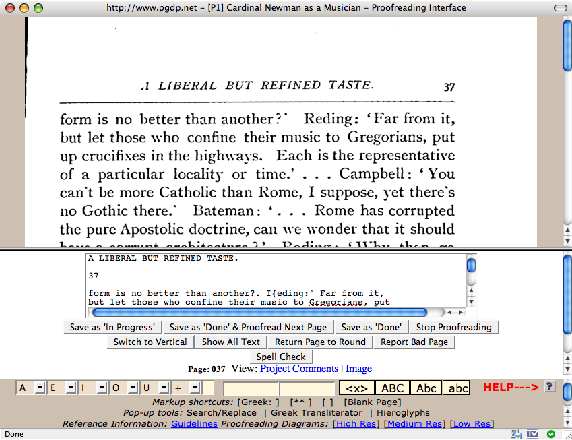
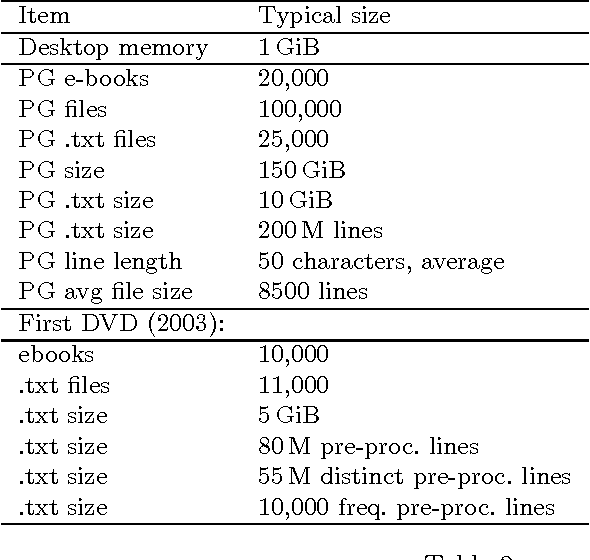
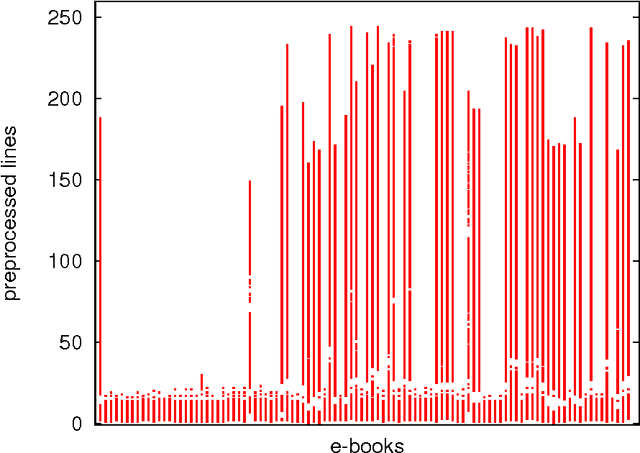
Collaborative work on unstructured or semi-structured documents, such as in literature corpora or source code, often involves agreed upon templates containing metadata. These templates are not consistent across users and over time. Rule-based parsing of these templates is expensive to maintain and tends to fail as new documents are added. Statistical techniques based on frequent occurrences have the potential to identify automatically a large fraction of the templates, thus reducing the burden on the programmers. We investigate the case of the Project Gutenberg corpus, where most documents are in ASCII format with preambles and epilogues that are often copied and pasted or manually typed. We show that a statistical approach can solve most cases though some documents require knowledge of English. We also survey various technical solutions that make our approach applicable to large data sets.

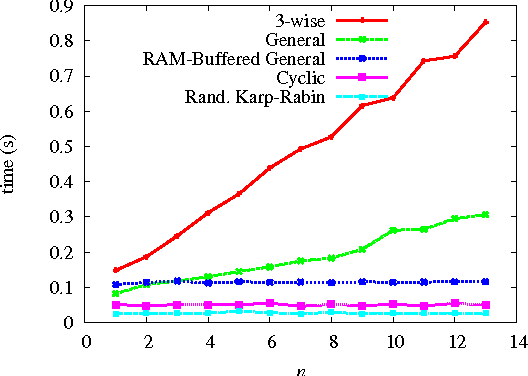
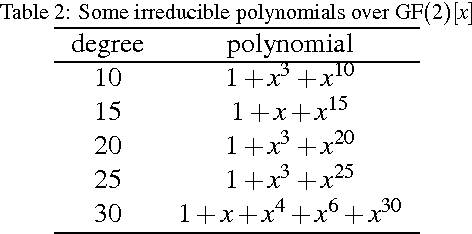
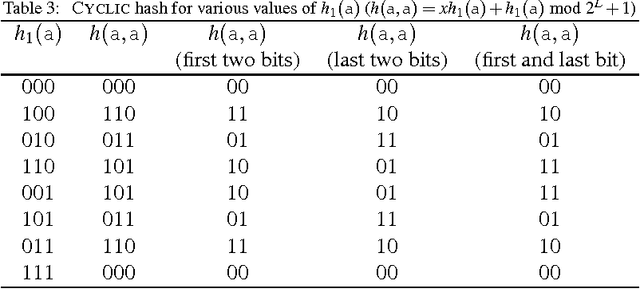
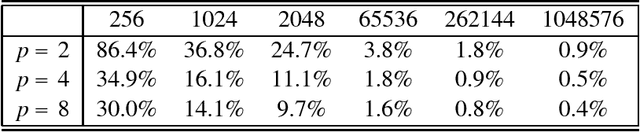
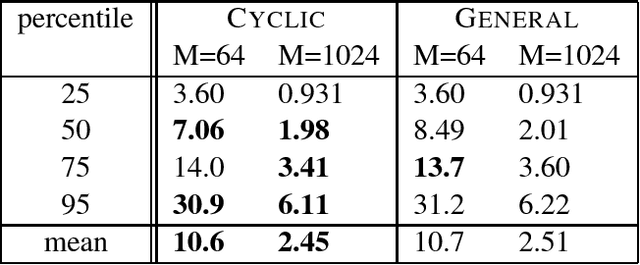
Recursive n-gram hashing is pairwise independent, at best

Many applications use sequences of n consecutive symbols (n-grams). Hashing these n-grams can be a performance bottleneck. For more speed, recursive hash families compute hash values by updating previous values. We prove that recursive hash families cannot be more than pairwise independent. While hashing by irreducible polynomials is pairwise independent, our implementations either run in time O(n) or use an exponential amount of memory. As a more scalable alternative, we make hashing by cyclic polynomials pairwise independent by ignoring n-1 bits. Experimentally, we show that hashing by cyclic polynomials is is twice as fast as hashing by irreducible polynomials. We also show that randomized Karp-Rabin hash families are not pairwise independent.

One-Pass, One-Hash n-Gram Statistics Estimation

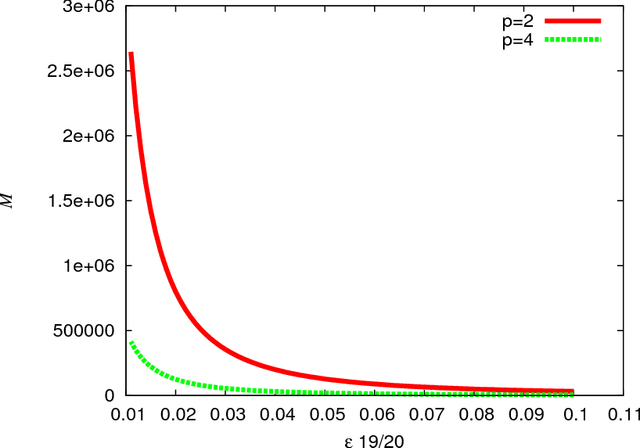
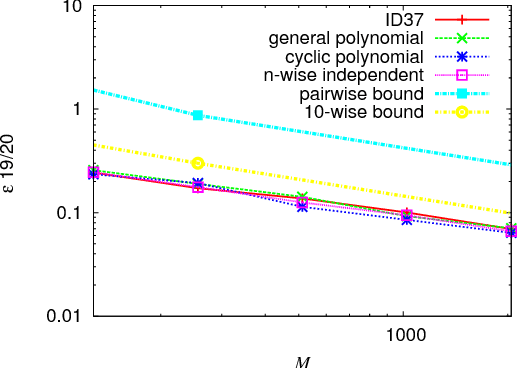
In multimedia, text or bioinformatics databases, applications query sequences of n consecutive symbols called n-grams. Estimating the number of distinct n-grams is a view-size estimation problem. While view sizes can be estimated by sampling under statistical assumptions, we desire an unassuming algorithm with universally valid accuracy bounds. Most related work has focused on repeatedly hashing the data, which is prohibitive for large data sources. We prove that a one-pass one-hash algorithm is sufficient for accurate estimates if the hashing is sufficiently independent. To reduce costs further, we investigate recursive random hashing algorithms and show that they are sufficiently independent in practice. We compare our running times with exact counts using suffix arrays and show that, while we use hardly any storage, we are an order of magnitude faster. The approach further is extended to a one-pass/one-hash computation of n-gram entropy and iceberg counts. The experiments use a large collection of English text from the Gutenberg Project as well as synthetic data.