One-Pass, One-Hash n-Gram Statistics Estimation
Paper and Code
Feb 04, 2014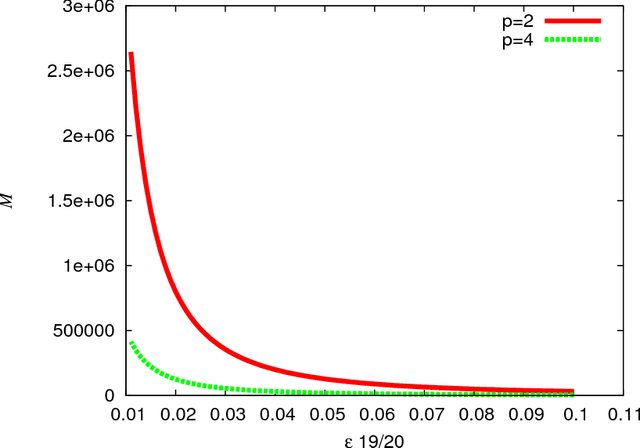
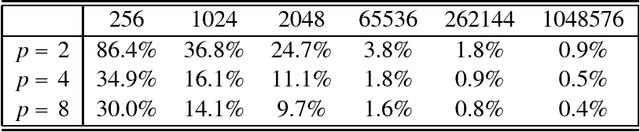
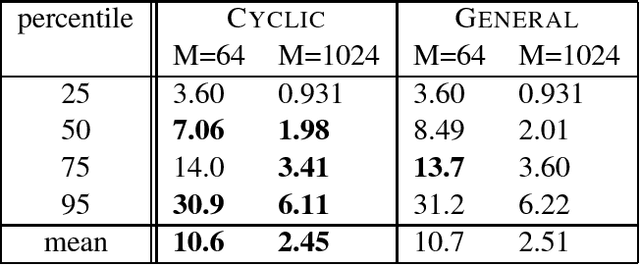
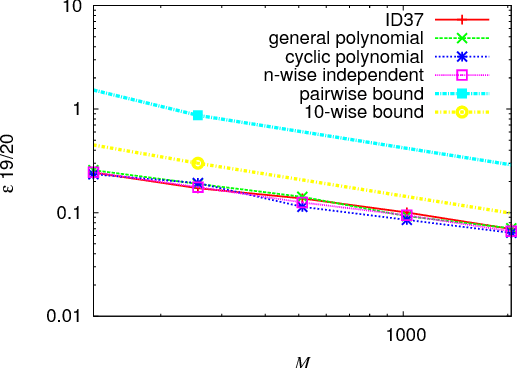
In multimedia, text or bioinformatics databases, applications query sequences of n consecutive symbols called n-grams. Estimating the number of distinct n-grams is a view-size estimation problem. While view sizes can be estimated by sampling under statistical assumptions, we desire an unassuming algorithm with universally valid accuracy bounds. Most related work has focused on repeatedly hashing the data, which is prohibitive for large data sources. We prove that a one-pass one-hash algorithm is sufficient for accurate estimates if the hashing is sufficiently independent. To reduce costs further, we investigate recursive random hashing algorithms and show that they are sufficiently independent in practice. We compare our running times with exact counts using suffix arrays and show that, while we use hardly any storage, we are an order of magnitude faster. The approach further is extended to a one-pass/one-hash computation of n-gram entropy and iceberg counts. The experiments use a large collection of English text from the Gutenberg Project as well as synthetic data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge