Bridging the gap to real-world for network intrusion detection systems with data-centric approach

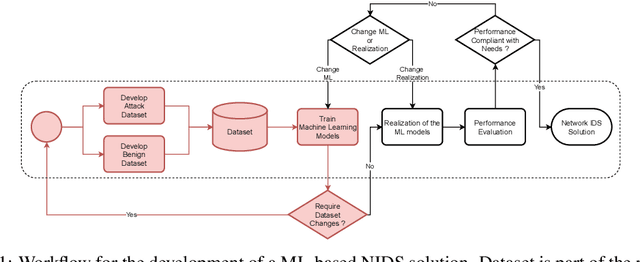
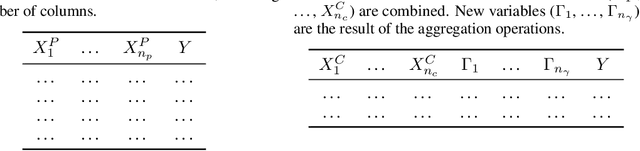
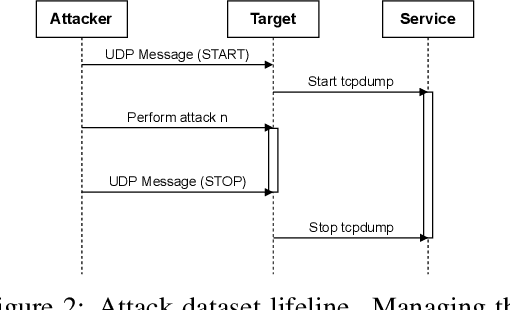
Most research using machine learning (ML) for network intrusion detection systems (NIDS) uses well-established datasets such as KDD-CUP99, NSL-KDD, UNSW-NB15, and CICIDS-2017. In this context, the possibilities of machine learning techniques are explored, aiming for metrics improvements compared to the published baselines (model-centric approach). However, those datasets present some limitations as aging that make it unfeasible to transpose those ML-based solutions to real-world applications. This paper presents a systematic data-centric approach to address the current limitations of NIDS research, specifically the datasets. This approach generates NIDS datasets composed of the most recent network traffic and attacks, with the labeling process integrated by design.

A-star path planning simulation for UAS Traffic Management application

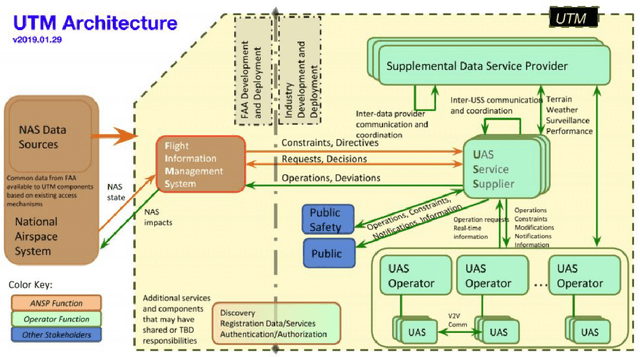
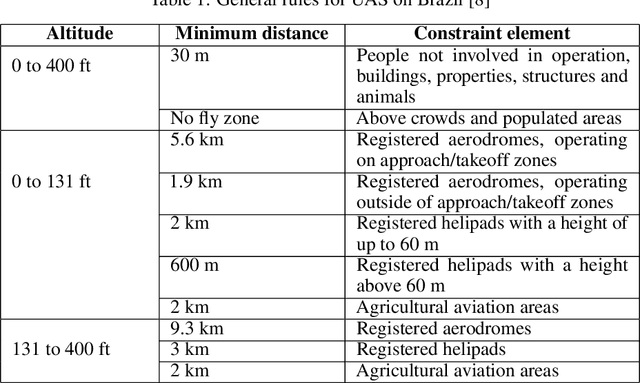
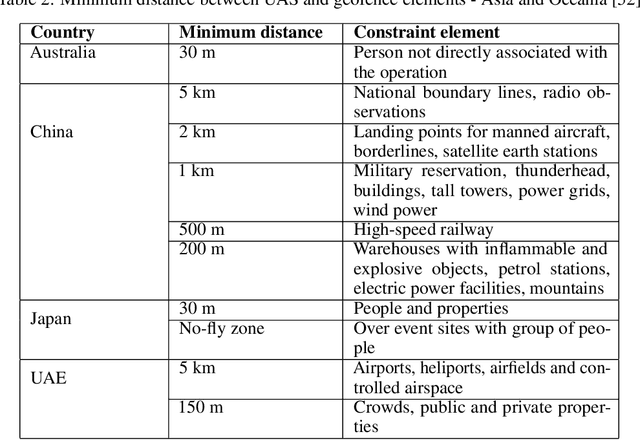
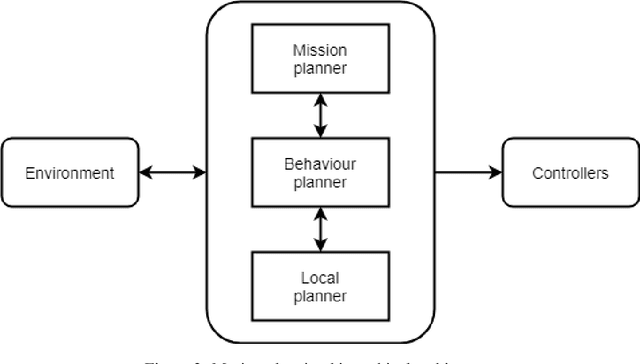
This paper presents a Robot Operating System and Gazebo application to calculate and simulate an optimal route for a drone in an urban environment by developing new ROS packages and executing them along with open-source tools. Firstly, the current regulations about UAS are presented to guide the building of the simulated environment, and multiple path planning algorithms are reviewed to guide the search method selection. After selecting the A-star algorithm, both the 2D and 3D versions of them were implemented in this paper, with both Manhattan and Euclidean distances heuristics. The performance of these algorithms was evaluated considering the distance to be covered by the drone and the execution time of the route planning method, aiming to support algorithm's choice based on the environment in which it will be applied. The algorithm execution time was 3.2 and 17.2 higher when using the Euclidean distance for the 2D and 3D A-star algorithm, respectively. Along with the performance analysis of the algorithm, this paper is also the first step for building a complete UAS Traffic Management (UTM) system simulation using ROS and Gazebo.

Total Variation Applications in Computer Vision

The objectives of this chapter are: (i) to introduce a concise overview of regularization; (ii) to define and to explain the role of a particular type of regularization called total variation norm (TV-norm) in computer vision tasks; (iii) to set up a brief discussion on the mathematical background of TV methods; and (iv) to establish a relationship between models and a few existing methods to solve problems cast as TV-norm. For the most part, image-processing algorithms blur the edges of the estimated images, however TV regularization preserves the edges with no prior information on the observed and the original images. The regularization scalar parameter {\lambda} controls the amount of regularization allowed and it is an essential to obtain a high-quality regularized output. A wide-ranging review of several ways to put into practice TV regularization as well as its advantages and limitations are discussed.