IPatch: A Multi-Resolution Transformer Architecture for Robust Time-Series Forecasting

Accurate forecasting of multivariate time series remains challenging due to the need to capture both short-term fluctuations and long-range temporal dependencies. Transformer-based models have emerged as a powerful approach, but their performance depends critically on the representation of temporal data. Traditional point-wise representations preserve individual time-step information, enabling fine-grained modeling, yet they tend to be computationally expensive and less effective at modeling broader contextual dependencies, limiting their scalability to long sequences. Patch-wise representations aggregate consecutive steps into compact tokens to improve efficiency and model local temporal dynamics, but they often discard fine-grained temporal details that are critical for accurate predictions in volatile or complex time series. We propose IPatch, a multi-resolution Transformer architecture that integrates both point-wise and patch-wise tokens, modeling temporal information at multiple resolutions. Experiments on 7 benchmark datasets demonstrate that IPatch consistently improves forecasting accuracy, robustness to noise, and generalization across various prediction horizons compared to single-representation baselines.

XStacking: Explanation-Guided Stacked Ensemble Learning

Ensemble Machine Learning (EML) techniques, especially stacking, have been shown to improve predictive performance by combining multiple base models. However, they are often criticized for their lack of interpretability. In this paper, we introduce XStacking, an effective and inherently explainable framework that addresses this limitation by integrating dynamic feature transformation with model-agnostic Shapley additive explanations. This enables stacked models to retain their predictive accuracy while becoming inherently explainable. We demonstrate the effectiveness of the framework on 29 datasets, achieving improvements in both the predictive effectiveness of the learning space and the interpretability of the resulting models. XStacking offers a practical and scalable solution for responsible ML.

A Survey on Cluster-based Federated Learning

As the industrial and commercial use of Federated Learning (FL) has expanded, so has the need for optimized algorithms. In settings were FL clients' data is non-independently and identically distributed (non-IID) and with highly heterogeneous distributions, the baseline FL approach seems to fall short. To tackle this issue, recent studies, have looked into personalized FL (PFL) which relaxes the implicit single-model constraint and allows for multiple hypotheses to be learned from the data or local models. Among the personalized FL approaches, cluster-based solutions (CFL) are particularly interesting whenever it is clear -through domain knowledge -that the clients can be separated into groups. In this paper, we study recent works on CFL, proposing: i) a classification of CFL solutions for personalization; ii) a structured review of literature iii) a review of alternative use cases for CFL. CCS Concepts: $\bullet$ General and reference $\rightarrow$ Surveys and overviews; $\bullet$ Computing methodologies $\rightarrow$ Machine learning; $\bullet$ Information systems $\rightarrow$ Clustering; $\bullet$ Security and privacy $\rightarrow$ Privacy-preserving protocols.

Comparative Evaluation of Clustered Federated Learning Method

Over recent years, Federated Learning (FL) has proven to be one of the most promising methods of distributed learning which preserves data privacy. As the method evolved and was confronted to various real-world scenarios, new challenges have emerged. One such challenge is the presence of highly heterogeneous (often referred as non-IID) data distributions among participants of the FL protocol. A popular solution to this hurdle is Clustered Federated Learning (CFL), which aims to partition clients into groups where the distribution are homogeneous. In the literature, state-of-the-art CFL algorithms are often tested using a few cases of data heterogeneities, without systematically justifying the choices. Further, the taxonomy used for differentiating the different heterogeneity scenarios is not always straightforward. In this paper, we explore the performance of two state-of-theart CFL algorithms with respect to a proposed taxonomy of data heterogeneities in federated learning (FL). We work with three image classification datasets and analyze the resulting clusters against the heterogeneity classes using extrinsic clustering metrics. Our objective is to provide a clearer understanding of the relationship between CFL performances and data heterogeneity scenarios.

DECWA : Density-Based Clustering using Wasserstein Distance

Clustering is a data analysis method for extracting knowledge by discovering groups of data called clusters. Among these methods, state-of-the-art density-based clustering methods have proven to be effective for arbitrary-shaped clusters. Despite their encouraging results, they suffer to find low-density clusters, near clusters with similar densities, and high-dimensional data. Our proposals are a new characterization of clusters and a new clustering algorithm based on spatial density and probabilistic approach. First of all, sub-clusters are built using spatial density represented as probability density function ($p.d.f$) of pairwise distances between points. A method is then proposed to agglomerate similar sub-clusters by using both their density ($p.d.f$) and their spatial distance. The key idea we propose is to use the Wasserstein metric, a powerful tool to measure the distance between $p.d.f$ of sub-clusters. We show that our approach outperforms other state-of-the-art density-based clustering methods on a wide variety of datasets.

Why Should I Choose You? AutoXAI: A Framework for Selecting and Tuning eXplainable AI Solutions

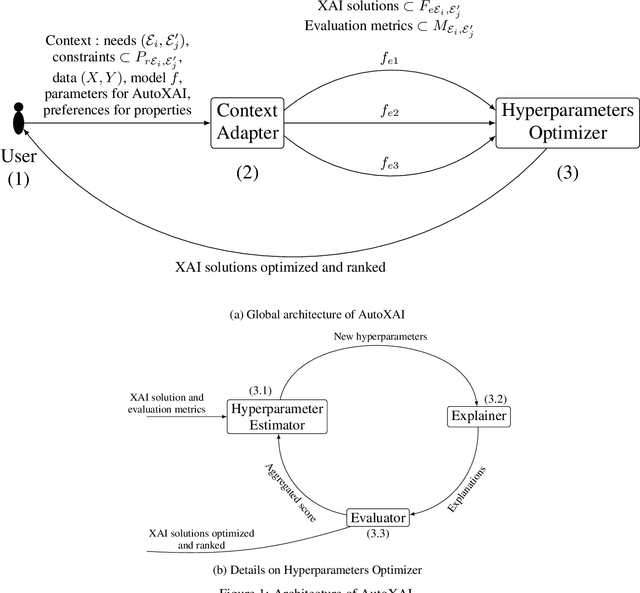
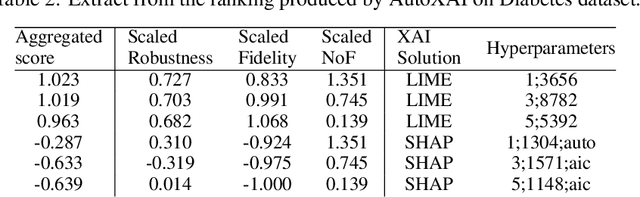
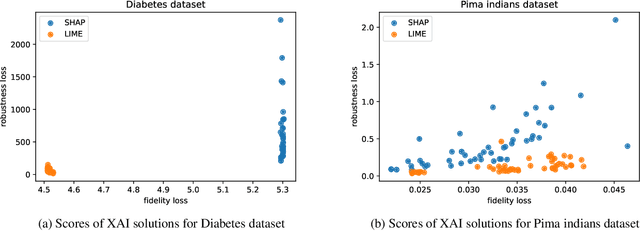
In recent years, a large number of XAI (eXplainable Artificial Intelligence) solutions have been proposed to explain existing ML (Machine Learning) models or to create interpretable ML models. Evaluation measures have recently been proposed and it is now possible to compare these XAI solutions. However, selecting the most relevant XAI solution among all this diversity is still a tedious task, especially when meeting specific needs and constraints. In this paper, we propose AutoXAI, a framework that recommends the best XAI solution and its hyperparameters according to specific XAI evaluation metrics while considering the user's context (dataset, ML model, XAI needs and constraints). It adapts approaches from context-aware recommender systems and strategies of optimization and evaluation from AutoML (Automated Machine Learning). We apply AutoXAI to two use cases, and show that it recommends XAI solutions adapted to the user's needs with the best hyperparameters matching the user's constraints.