Olivier Scaillet
A penalized two-pass regression to predict stock returns with time-varying risk premia
Aug 01, 2022Abstract:We develop a penalized two-pass regression with time-varying factor loadings. The penalization in the first pass enforces sparsity for the time-variation drivers while also maintaining compatibility with the no-arbitrage restrictions by regularizing appropriate groups of coefficients. The second pass delivers risk premia estimates to predict equity excess returns. Our Monte Carlo results and our empirical results on a large cross-sectional data set of US individual stocks show that penalization without grouping can yield to nearly all estimated time-varying models violating the no-arbitrage restrictions. Moreover, our results demonstrate that the proposed method reduces the prediction errors compared to a penalized approach without appropriate grouping or a time-invariant factor model.
Multi-Signal Approaches for Repeated Sampling Schemes in Inertial Sensor Calibration
May 17, 2021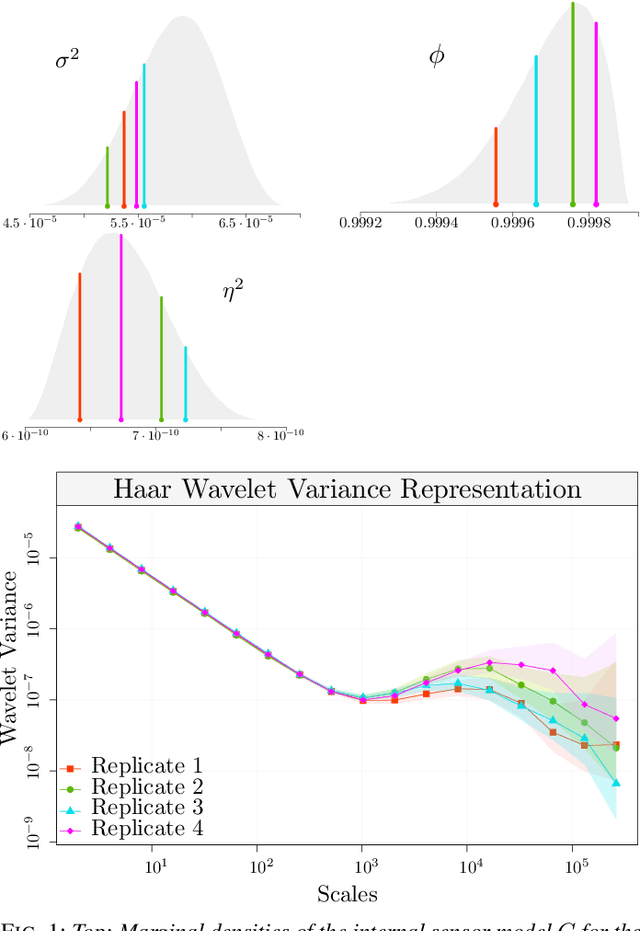
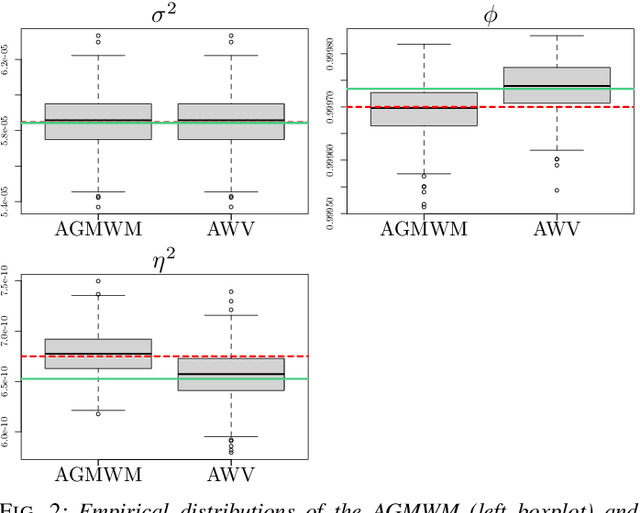
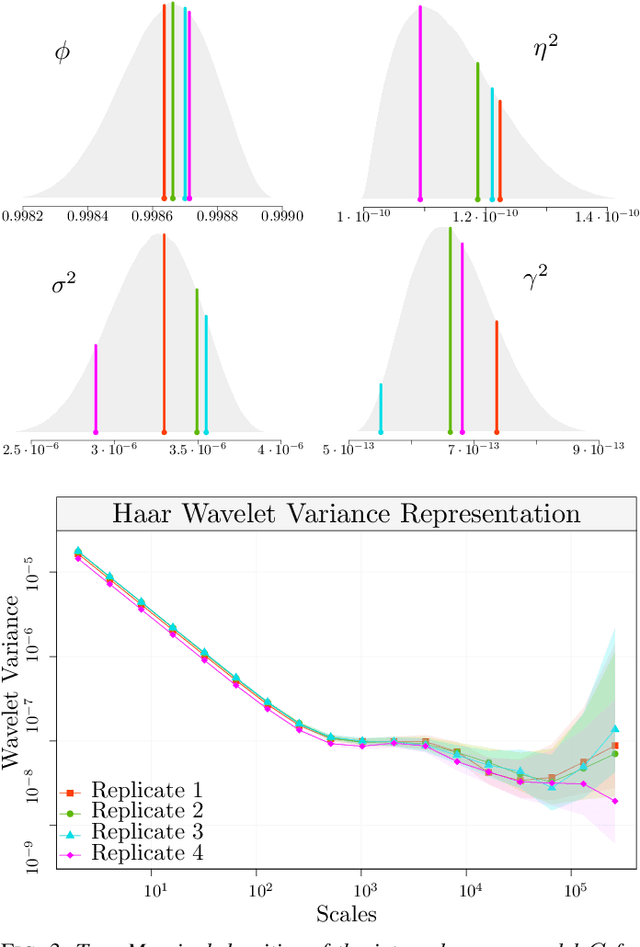
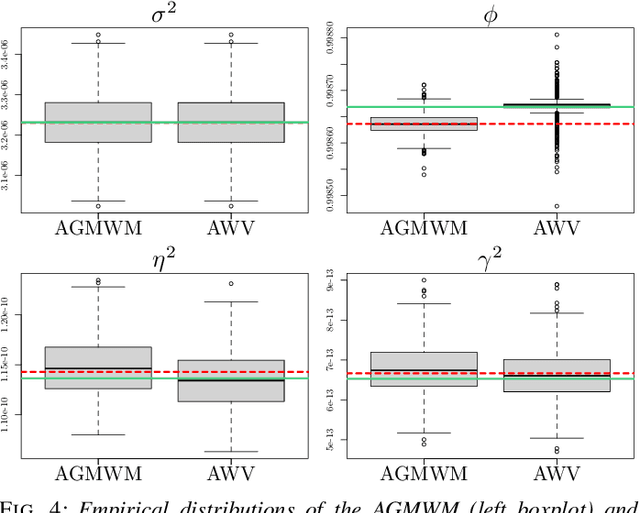
Abstract:The task of inertial sensor calibration has become increasingly important due to the growing use of low-cost inertial measurement units which are however characterized by measurement errors. Being widely employed in a variety of mass-market applications, there is considerable focus on compensating for these errors by taking into account the deterministic and stochastic factors that characterize them. In this paper, we focus on the stochastic part of the error signal where it is customary to record the latter and use the observed error signal to identify and estimate the stochastic models, often complex in nature, that underlie this process. However, it is often the case that these error signals are observed through a series of replicates for the same inertial sensor and equally often that these replicates have the same model structure but their parameters appear different between replicates. This phenomenon has not been taken into account by current stochastic calibration procedures which therefore can be conditioned by flawed parameter estimation. For this reason, this paper aims at studying different approaches for this problem and studying their properties to take into account parameter variation between replicates thereby improving measurement precision and navigation uncertainty quantification in the long run.
SWAG: A Wrapper Method for Sparse Learning
Jun 23, 2020



Abstract:Predictive power has always been the main research focus of learning algorithms. While the general approach for these algorithms is to consider all possible attributes in a dataset to best predict the response of interest, an important branch of research is focused on sparse learning. Indeed, in many practical settings we believe that only an extremely small combination of different attributes affect the response. However even sparse-learning methods can still preserve a high number of attributes in high-dimensional settings and possibly deliver inconsistent prediction performance. The latter methods can also be hard to interpret for researchers and practitioners, a problem which is even more relevant for the ``black-box''-type mechanisms of many learning approaches. Finally, there is often a problem of replicability since not all data-collection procedures measure (or observe) the same attributes and therefore cannot make use of proposed learners for testing purposes. To address all the previous issues, we propose to study a procedure that combines screening and wrapper methods and aims to find a library of extremely low-dimensional attribute combinations (with consequent low data collection and storage costs) in order to (i) match or improve the predictive performance of any particular learning method which uses all attributes as an input (including sparse learners); (ii) provide a low-dimensional network of attributes easily interpretable by researchers and practitioners; and (iii) increase the potential replicability of results due to a diversity of attribute combinations defining strong learners with equivalent predictive power. We call this algorithm ``Sparse Wrapper AlGorithm'' (SWAG).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge