Oleksandr Antonenko
A theory of incremental compression
Aug 10, 2019
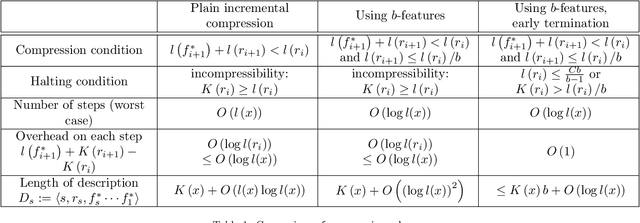
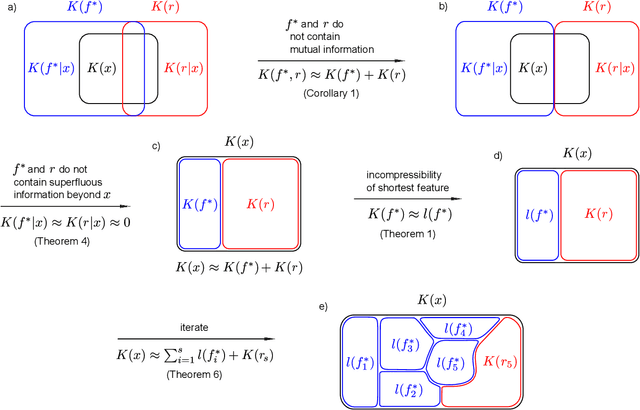
Abstract:The ability to find short representations, i.e. to compress data, is crucial for many intelligent systems. We present a theory of incremental compression showing that arbitrary data strings, that can be described by a set of features, can be compressed by searching for those features incrementally, which results in a partition of the information content of the string into a complete set of pairwise independent pieces. The description length of this partition turns out to be close to optimal in terms of the Kolmogorov complexity of the string. At the same time, the incremental nature of our method constitutes a major step toward faster compression compared to non-incremental versions of universal search, while still staying general. We further show that our concept of a feature is closely related to Martin-L\"of randomness tests, thereby formalizing the meaning of "property" for computable objects.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge