Arthur Franz
A theory of incremental compression
Aug 10, 2019
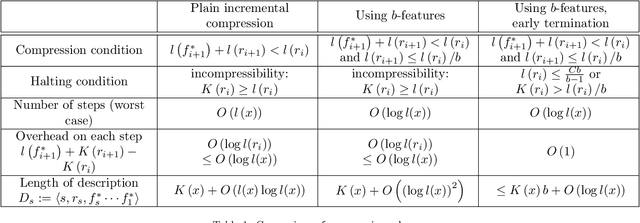
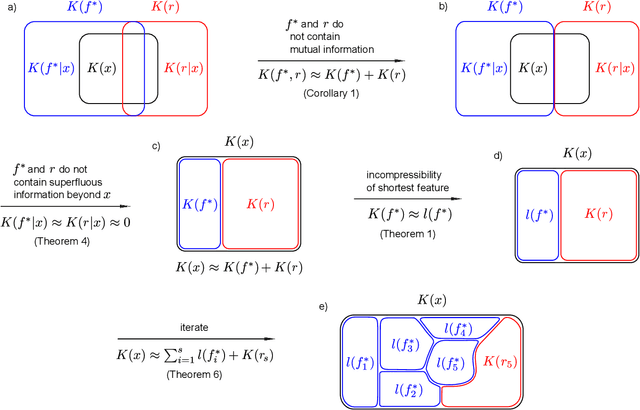
Abstract:The ability to find short representations, i.e. to compress data, is crucial for many intelligent systems. We present a theory of incremental compression showing that arbitrary data strings, that can be described by a set of features, can be compressed by searching for those features incrementally, which results in a partition of the information content of the string into a complete set of pairwise independent pieces. The description length of this partition turns out to be close to optimal in terms of the Kolmogorov complexity of the string. At the same time, the incremental nature of our method constitutes a major step toward faster compression compared to non-incremental versions of universal search, while still staying general. We further show that our concept of a feature is closely related to Martin-L\"of randomness tests, thereby formalizing the meaning of "property" for computable objects.
Artificial general intelligence through recursive data compression and grounded reasoning: a position paper
Jun 14, 2015


Abstract:This paper presents a tentative outline for the construction of an artificial, generally intelligent system (AGI). It is argued that building a general data compression algorithm solving all problems up to a complexity threshold should be the main thrust of research. A measure for partial progress in AGI is suggested. Although the details are far from being clear, some general properties for a general compression algorithm are fleshed out. Its inductive bias should be flexible and adapt to the input data while constantly searching for a simple, orthogonal and complete set of hypotheses explaining the data. It should recursively reduce the size of its representations thereby compressing the data increasingly at every iteration. Abstract Based on that fundamental ability, a grounded reasoning system is proposed. It is argued how grounding and flexible feature bases made of hypotheses allow for resourceful thinking. While the simulation of representation contents on the mental stage accounts for much of the power of propositional logic, compression leads to simple sets of hypotheses that allow the detection and verification of universally quantified statements. Abstract Together, it is highlighted how general compression and grounded reasoning could account for the birth and growth of first concepts about the world and the commonsense reasoning about them.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge