Monolingual Probabilistic Programming Using Generalized Coroutines

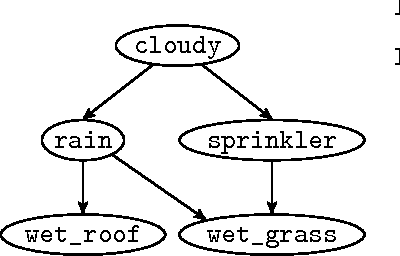
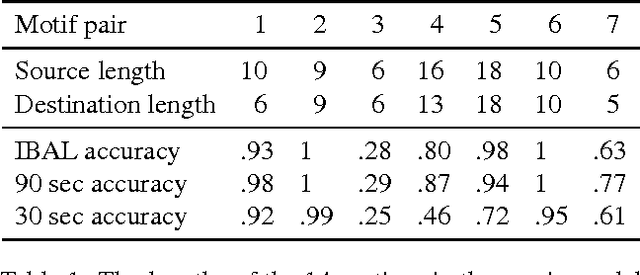
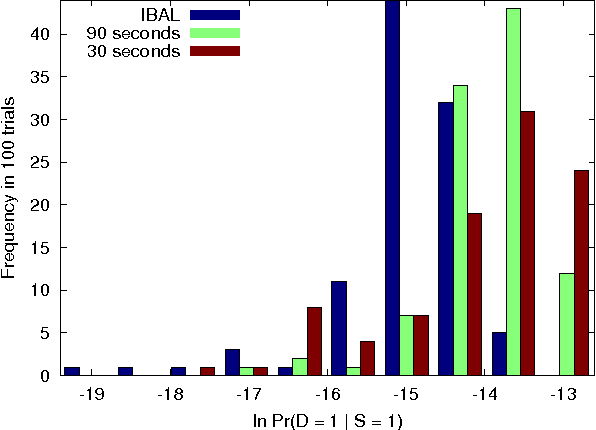
Probabilistic programming languages and modeling toolkits are two modular ways to build and reuse stochastic models and inference procedures. Combining strengths of both, we express models and inference as generalized coroutines in the same general-purpose language. We use existing facilities of the language, such as rich libraries, optimizing compilers, and types, to develop concise, declarative, and realistic models with competitive performance on exact and approximate inference. In particular, a wide range of models can be expressed using memoization. Because deterministic parts of models run at full speed, custom inference procedures are trivial to incorporate, and inference procedures can reason about themselves without interpretive overhead. Within this framework, we introduce a new, general algorithm for importance sampling with look-ahead.

Type Arithmetics: Computation based on the theory of types

The present paper shows meta-programming turn programming, which is rich enough to express arbitrary arithmetic computations. We demonstrate a type system that implements Peano arithmetics, slightly generalized to negative numbers. Certain types in this system denote numerals. Arithmetic operations on such types-numerals - addition, subtraction, and even division - are expressed as type reduction rules executed by a compiler. A remarkable trait is that division by zero becomes a type error - and reported as such by a compiler.

Image Compression with Iterated Function Systems, Finite Automata and Zerotrees: Grand Unification

Fractal image compression, Culik's image compression and zerotree prediction coding of wavelet image decomposition coefficients succeed only because typical images being compressed possess a significant degree of self-similarity. Besides the common concept, these methods turn out to be even more tightly related, to the point of algorithmical reducibility of one technique to another. The goal of the present paper is to demonstrate these relations. The paper offers a plain-term interpretation of Culik's image compression, in regular image processing terms, without resorting to finite state machines and similar lofty language. The interpretation is shown to be algorithmically related to an IFS fractal image compression method: an IFS can be exactly transformed into Culik's image code. Using this transformation, we will prove that in a self-similar (part of an) image any zero wavelet coefficient is the root of a zerotree, or its branch. The paper discusses the zerotree coding of (wavelet/projection) coefficients as a common predictor/corrector, applied vertically through different layers of a multiresolutional decomposition, rather than within the same view. This interpretation leads to an insight into the evolution of image compression techniques: from a causal single-layer prediction, to non-causal same-view predictions (wavelet decomposition among others) and to a causal cross-layer prediction (zero-trees, Culik's method).