Parametric Amplifier Matching Using Legendre Prototypes

In this note we describe Josephson parametric amplifier (JPA) matching networks based on Legendre polynomials. These networks typically exhibit lower ripple and gentler roll-off than Chebyshev networks with similar parameters, and can be viewed as bridging the gap between Butterworth and Chebyshev ones. We tabulate prototype coefficients for parametric amplifiers based on Legendre polynomials with a range of gain and ripple parameters, and for a range of network orders. We also use this opportunity to further illustrate the synthesis of these networks based on methods from previous work, and synthesize a prototype JPA with 20dB gain at a center frequency of 5GHz with a bandwidth of 500MHz.

Synthesis of parametrically-coupled networks

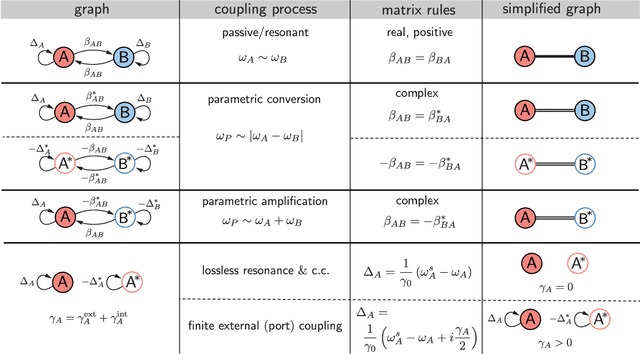
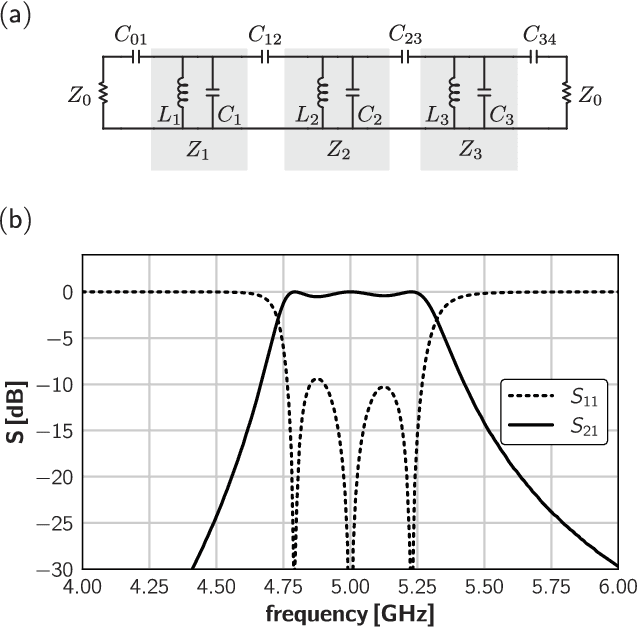
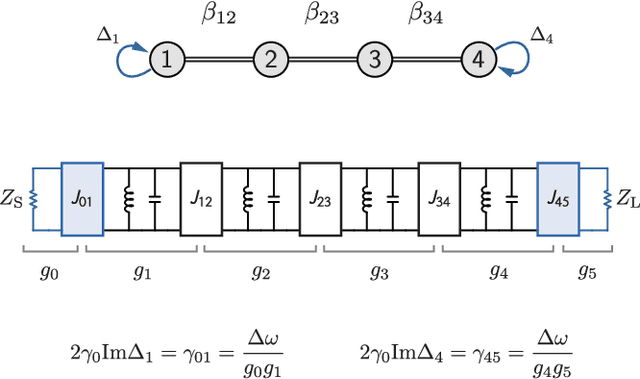
We show that a common language can be used to unify the description of parametrically-coupled circuits--parametric amplifiers, frequency converters, and parametric nonreciprocal devices--with that of band-pass filter and impedance matching networks. This enables one to readily adapt network synthesis methods from microwave engineering in the design of parametrically-coupled devices having prescribed transfer characteristics, e.g. gain, bandwidth, return loss, and isolation. We review basic practical aspects of coupled mode theory and filter synthesis, and then show how to apply both, on an equal footing, to the design of multi-pole, broadband parametric and non-reciprocal networks. We supplement the discussion with a range of examples and reference designs.

Learning Non-Markovian Quantum Noise from Moiré-Enhanced Swap Spectroscopy with Deep Evolutionary Algorithm

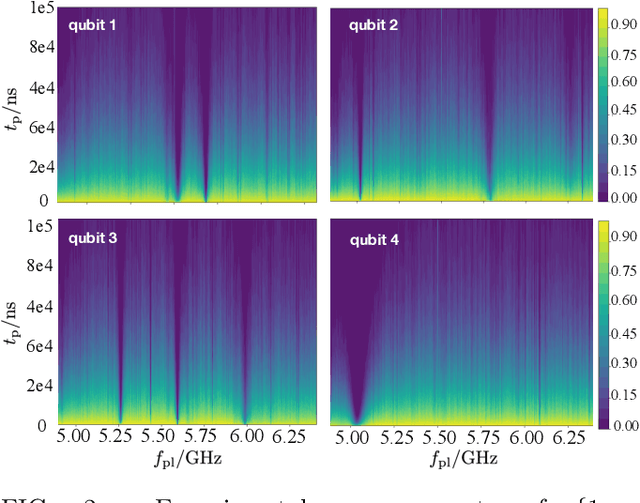
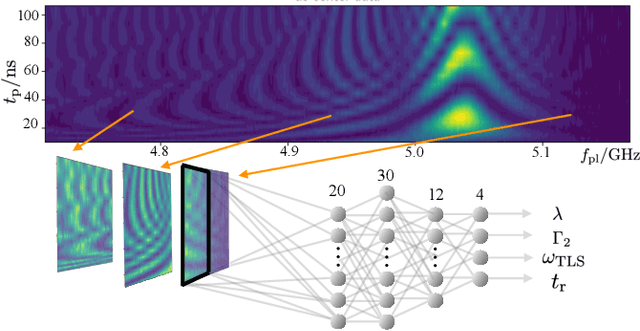
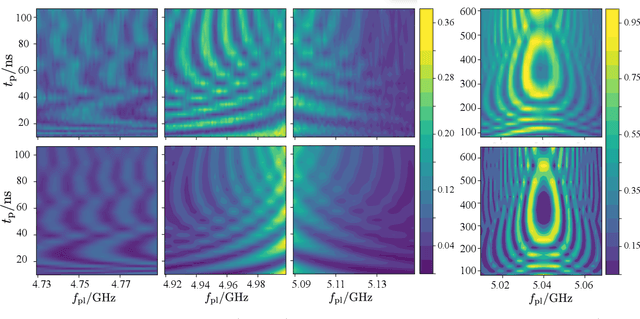
Two-level-system (TLS) defects in amorphous dielectrics are a major source of noise and decoherence in solid-state qubits. Gate-dependent non-Markovian errors caused by TLS-qubit coupling are detrimental to fault-tolerant quantum computation and have not been rigorously treated in the existing literature. In this work, we derive the non-Markovian dynamics between TLS and qubits during a SWAP-like two-qubit gate and the associated average gate fidelity for frequency-tunable Transmon qubits. This gate dependent error model facilitates using qubits as sensors to simultaneously learn practical imperfections in both the qubit's environment and control waveforms. We combine the-state-of-art machine learning algorithm with Moir\'{e}-enhanced swap spectroscopy to achieve robust learning using noisy experimental data. Deep neural networks are used to represent the functional map from experimental data to TLS parameters and are trained through an evolutionary algorithm. Our method achieves the highest learning efficiency and robustness against experimental imperfections to-date, representing an important step towards in-situ quantum control optimization over environmental and control defects.