Sampling-Free Privacy Accounting for Matrix Mechanisms under Random Allocation

We study privacy amplification for differentially private model training with matrix factorization under random allocation (also known as the balls-in-bins model). Recent work by Choquette-Choo et al. (2025) proposes a sampling-based Monte Carlo approach to compute amplification parameters in this setting. However, their guarantees either only hold with some high probability or require random abstention by the mechanism. Furthermore, the required number of samples for ensuring $(ε,δ)$-DP is inversely proportional to $δ$. In contrast, we develop sampling-free bounds based on Rényi divergence and conditional composition. The former is facilitated by a dynamic programming formulation to efficiently compute the bounds. The latter complements it by offering stronger privacy guarantees for small $ε$, where Rényi divergence bounds inherently lead to an over-approximation. Our framework applies to arbitrary banded and non-banded matrices. Through numerical comparisons, we demonstrate the efficacy of our approach across a broad range of matrix mechanisms used in research and practice.

Banded Square Root Matrix Factorization for Differentially Private Model Training

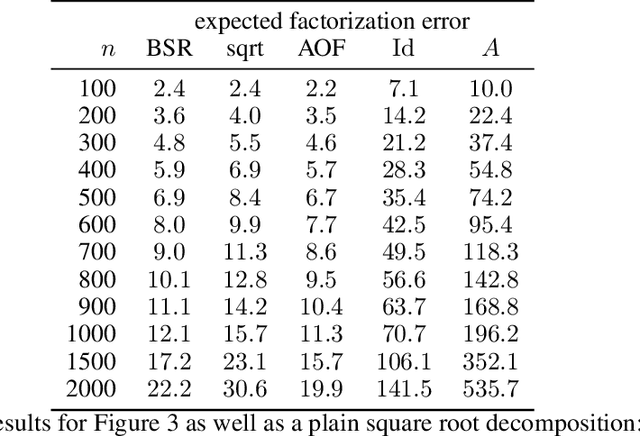
Current state-of-the-art methods for differentially private model training are based on matrix factorization techniques. However, these methods suffer from high computational overhead because they require numerically solving a demanding optimization problem to determine an approximately optimal factorization prior to the actual model training. In this work, we present a new matrix factorization approach, BSR, which overcomes this computational bottleneck. By exploiting properties of the standard matrix square root, BSR allows to efficiently handle also large-scale problems. For the key scenario of stochastic gradient descent with momentum and weight decay, we even derive analytical expressions for BSR that render the computational overhead negligible. We prove bounds on the approximation quality that hold both in the centralized and in the federated learning setting. Our numerical experiments demonstrate that models trained using BSR perform on par with the best existing methods, while completely avoiding their computational overhead.