Niharika Gauraha
Combining Prediction Intervals on Multi-Source Non-Disclosed Regression Datasets
Aug 15, 2019

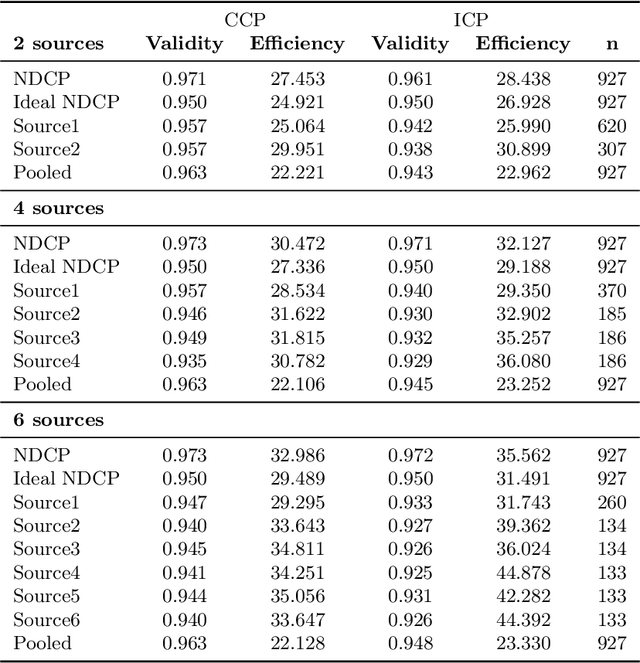
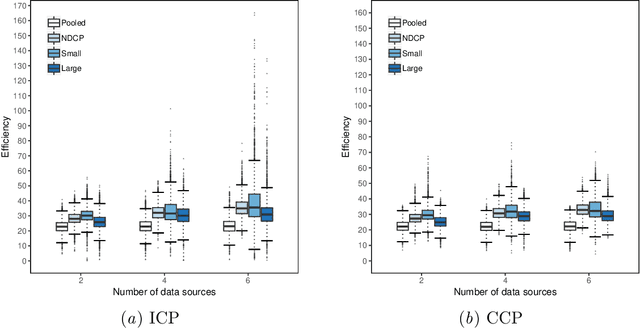
Abstract:Conformal Prediction is a framework that produces prediction intervals based on the output from a machine learning algorithm. In this paper we explore the case when training data is made up of multiple parts available in different sources that cannot be pooled. We here consider the regression case and propose a method where a conformal predictor is trained on each data source independently, and where the prediction intervals are then combined into a single interval. We call the approach Non-Disclosed Conformal Prediction (NDCP), and we evaluate it on a regression dataset from the UCI machine learning repository using support vector regression as the underlying machine learning algorithm, with varying number of data sources and sizes. The results show that the proposed method produces conservatively valid prediction intervals, and while we cannot retain the same efficiency as when all data is used, efficiency is improved through the proposed approach as compared to predicting using a single arbitrarily chosen source.
A Limitation of V-Matrix based Methods
Aug 27, 2018Abstract:To estimate the conditional probability functions based on the direct problem setting, V-matrix based method was proposed. We construct V-matrix based constrained quadratic programming problems for which the inequality constraints are inconsistent. In particular, we would like to present that the constrained quadratic optimization problem for conditional probability estimation using V-matrix method may not have a consistent solution always.
Aggregating Predictions on Multiple Non-disclosed Datasets using Conformal Prediction
Jun 14, 2018



Abstract:Conformal Prediction is a machine learning methodology that produces valid prediction regions under mild conditions. In this paper, we explore the application of making predictions over multiple data sources of different sizes without disclosing data between the sources. We propose that each data source applies a transductive conformal predictor independently using the local data, and that the individual predictions are then aggregated to form a combined prediction region. We demonstrate the method on several data sets, and show that the proposed method produces conservatively valid predictions and reduces the variance in the aggregated predictions. We also study the effect that the number of data sources and size of each source has on aggregated predictions, as compared with equally sized sources and pooled data.
conformalClassification: A Conformal Prediction R Package for Classification
Apr 16, 2018Abstract:The conformalClassification package implements Transductive Conformal Prediction (TCP) and Inductive Conformal Prediction (ICP) for classification problems. Conformal Prediction (CP) is a framework that complements the predictions of machine learning algorithms with reliable measures of confidence. TCP gives results with higher validity than ICP, however ICP is computationally faster than TCP. The package conformalClassification is built upon the random forest method, where votes of the random forest for each class are considered as the conformity scores for each data point. Although the main aim of the conformalClassification package is to generate CP errors (p-values) for classification problems, the package also implements various diagnostic measures such as deviation from validity, error rate, efficiency, observed fuzziness and calibration plots. In future releases, we plan to extend the package to use other machine learning algorithms, (e.g. support vector machines) for model fitting.
Conformal Prediction in Learning Under Privileged Information Paradigm with Applications in Drug Discovery
Apr 04, 2018



Abstract:This paper explores conformal prediction in the learning under privileged information (LUPI) paradigm. We use the SVM+ realization of LUPI in an inductive conformal predictor, and apply it to the MNIST benchmark dataset and three datasets in drug discovery. The results show that using privileged information produces valid models and improves efficiency compared to standard SVM, however the improvement varies between the tested datasets and is not substantial in the drug discovery applications. More importantly, using SVM+ in a conformal prediction framework enables valid prediction intervals at specified significance levels.
Efficient Clustering of Correlated Variables and Variable Selection in High-Dimensional Linear Models
Mar 11, 2016



Abstract:In this paper, we introduce Adaptive Cluster Lasso(ACL) method for variable selection in high dimensional sparse regression models with strongly correlated variables. To handle correlated variables, the concept of clustering or grouping variables and then pursuing model fitting is widely accepted. When the dimension is very high, finding an appropriate group structure is as difficult as the original problem. The ACL is a three-stage procedure where, at the first stage, we use the Lasso(or its adaptive or thresholded version) to do initial selection, then we also include those variables which are not selected by the Lasso but are strongly correlated with the variables selected by the Lasso. At the second stage we cluster the variables based on the reduced set of predictors and in the third stage we perform sparse estimation such as Lasso on cluster representatives or the group Lasso based on the structures generated by clustering procedure. We show that our procedure is consistent and efficient in finding true underlying population group structure(under assumption of irrepresentable and beta-min conditions). We also study the group selection consistency of our method and we support the theory using simulated and pseudo-real dataset examples.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge