Adaptive Conformal Prediction by Reweighting Nonconformity Score

Despite attractive theoretical guarantees and practical successes, Predictive Interval (PI) given by Conformal Prediction (CP) may not reflect the uncertainty of a given model. This limitation arises from CP methods using a constant correction for all test points, disregarding their individual uncertainties, to ensure coverage properties. To address this issue, we propose using a Quantile Regression Forest (QRF) to learn the distribution of nonconformity scores and utilizing the QRF's weights to assign more importance to samples with residuals similar to the test point. This approach results in PI lengths that are more aligned with the model's uncertainty. In addition, the weights learnt by the QRF provide a partition of the features space, allowing for more efficient computations and improved adaptiveness of the PI through groupwise conformalization. Our approach enjoys an assumption-free finite sample marginal and training-conditional coverage, and under suitable assumptions, it also ensures conditional coverage. Our methods work for any nonconformity score and are available as a Python package. We conduct experiments on simulated and real-world data that demonstrate significant improvements compared to existing methods.

Rethinking Counterfactual Explanations as Local and Regional Counterfactual Policies

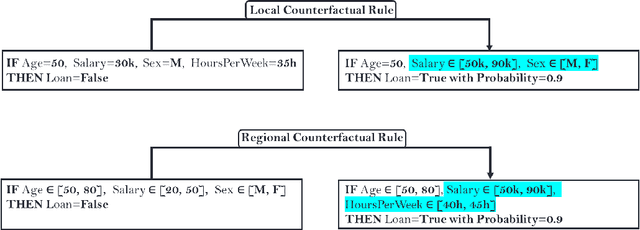
Among the challenges not yet resolved for Counterfactual Explanations (CE), there are stability, synthesis of the various CE and the lack of plausibility/sparsity guarantees. From a more practical point of view, recent studies show that the prescribed counterfactual recourses are often not implemented exactly by the individuals and demonstrate that most state-of-the-art CE algorithms are very likely to fail in this noisy environment. To address these issues, we propose a probabilistic framework that gives a sparse local counterfactual rule for each observation: we provide rules that give a range of values that can change the decision with a given high probability instead of giving diverse CE. In addition, the recourses derived from these rules are robust by construction. These local rules are aggregated into a regional counterfactual rule to ensure the stability of the counterfactual explanations across observations. Our local and regional rules guarantee that the recourses are faithful to the data distribution because our rules use a consistent estimator of the probabilities of changing the decision based on a Random Forest. In addition, these probabilities give interpretable and sparse rules as we select the smallest set of variables having a given probability of changing the decision. Codes for computing our counterfactual rules are available, and we compare their relevancy with standard CE and recent similar attempts.

Consistent Sufficient Explanations and Minimal Local Rules for explaining regression and classification models

To explain the decision of any model, we extend the notion of probabilistic Sufficient Explanations (P-SE). For each instance, this approach selects the minimal subset of features that is sufficient to yield the same prediction with high probability, while removing other features. The crux of P-SE is to compute the conditional probability of maintaining the same prediction. Therefore, we introduce an accurate and fast estimator of this probability via random Forests for any data $(\boldsymbol{X}, Y)$ and show its efficiency through a theoretical analysis of its consistency. As a consequence, we extend the P-SE to regression problems. In addition, we deal with non-binary features, without learning the distribution of $X$ nor having the model for making predictions. Finally, we introduce local rule-based explanations for regression/classification based on the P-SE and compare our approaches w.r.t other explainable AI methods. These methods are publicly available as a Python package at \url{www.github.com/salimamoukou/acv00}.