Rethinking Counterfactual Explanations as Local and Regional Counterfactual Policies
Paper and Code
Sep 29, 2022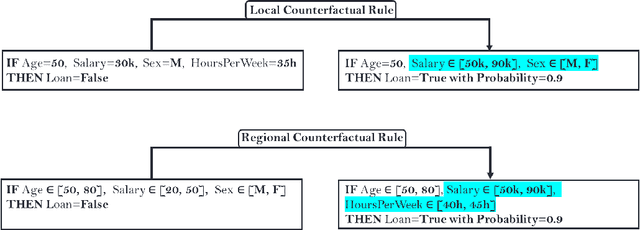

Among the challenges not yet resolved for Counterfactual Explanations (CE), there are stability, synthesis of the various CE and the lack of plausibility/sparsity guarantees. From a more practical point of view, recent studies show that the prescribed counterfactual recourses are often not implemented exactly by the individuals and demonstrate that most state-of-the-art CE algorithms are very likely to fail in this noisy environment. To address these issues, we propose a probabilistic framework that gives a sparse local counterfactual rule for each observation: we provide rules that give a range of values that can change the decision with a given high probability instead of giving diverse CE. In addition, the recourses derived from these rules are robust by construction. These local rules are aggregated into a regional counterfactual rule to ensure the stability of the counterfactual explanations across observations. Our local and regional rules guarantee that the recourses are faithful to the data distribution because our rules use a consistent estimator of the probabilities of changing the decision based on a Random Forest. In addition, these probabilities give interpretable and sparse rules as we select the smallest set of variables having a given probability of changing the decision. Codes for computing our counterfactual rules are available, and we compare their relevancy with standard CE and recent similar attempts.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge