Nicolas Berkouk
Singular Value Representation: A New Graph Perspective On Neural Networks
Feb 16, 2023



Abstract:We introduce the Singular Value Representation (SVR), a new method to represent the internal state of neural networks using SVD factorization of the weights. This construction yields a new weighted graph connecting what we call spectral neurons, that correspond to specific activation patterns of classical neurons. We derive a precise statistical framework to discriminate meaningful connections between spectral neurons for fully connected and convolutional layers. To demonstrate the usefulness of our approach for machine learning research, we highlight two discoveries we made using the SVR. First, we highlight the emergence of a dominant connection in VGG networks that spans multiple deep layers. Second, we witness, without relying on any input data, that batch normalization can induce significant connections between near-kernels of deep layers, leading to a remarkable spontaneous sparsification phenomenon.
Persformer: A Transformer Architecture for Topological Machine Learning
Dec 30, 2021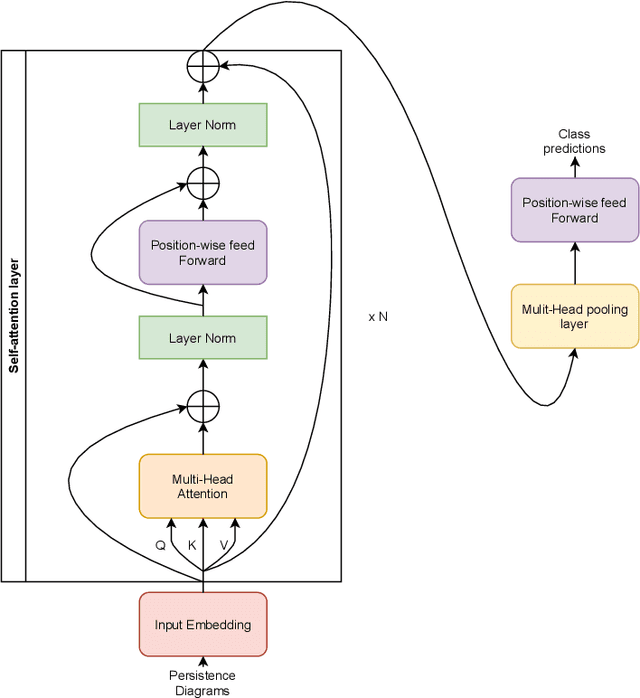



Abstract:One of the main challenges of Topological Data Analysis (TDA) is to extract features from persistent diagrams directly usable by machine learning algorithms. Indeed, persistence diagrams are intrinsically (multi-)sets of points in R2 and cannot be seen in a straightforward manner as vectors. In this article, we introduce Persformer, the first Transformer neural network architecture that accepts persistence diagrams as input. The Persformer architecture significantly outperforms previous topological neural network architectures on classical synthetic benchmark datasets. Moreover, it satisfies a universal approximation theorem. This allows us to introduce the first interpretability method for topological machine learning, which we explore in two examples.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge