Towards Information Theory-Based Discovery of Equivariances

The presence of symmetries imposes a stringent set of constraints on a system. This constrained structure allows intelligent agents interacting with such a system to drastically improve the efficiency of learning and generalization, through the internalisation of the system's symmetries into their information-processing. In parallel, principled models of complexity-constrained learning and behaviour make increasing use of information-theoretic methods. Here, we wish to marry these two perspectives and understand whether and in which form the information-theoretic lens can "see" the effect of symmetries of a system. For this purpose, we propose a novel variant of the Information Bottleneck principle, which has served as a productive basis for many principled studies of learning and information-constrained adaptive behaviour. We show (in the discrete case) that our approach formalises a certain duality between symmetry and information parsimony: namely, channel equivariances can be characterised by the optimal mutual information-preserving joint compression of the channel's input and output. This information-theoretic treatment furthermore suggests a principled notion of "soft" equivariance, whose "coarseness" is measured by the amount of input-output mutual information preserved by the corresponding optimal compression. This new notion offers a bridge between the field of bounded rationality and the study of symmetries in neural representations. The framework may also allow (exact and soft) equivariances to be automatically discovered.

A space of goals: the cognitive geometry of informationally bounded agents

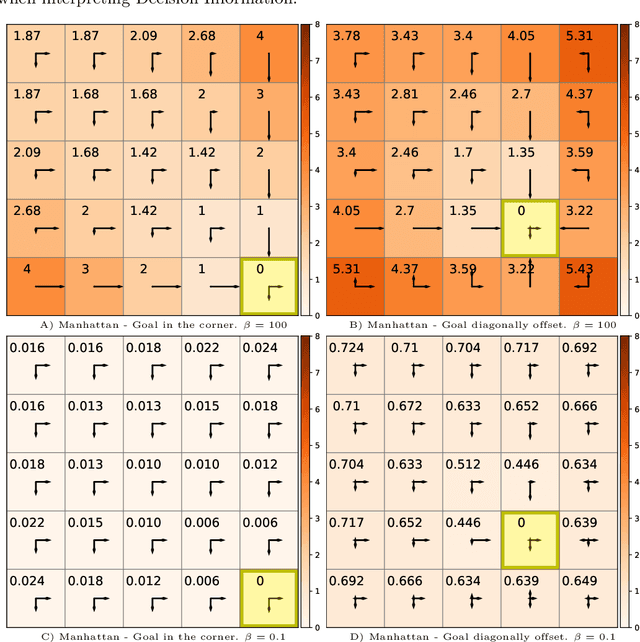
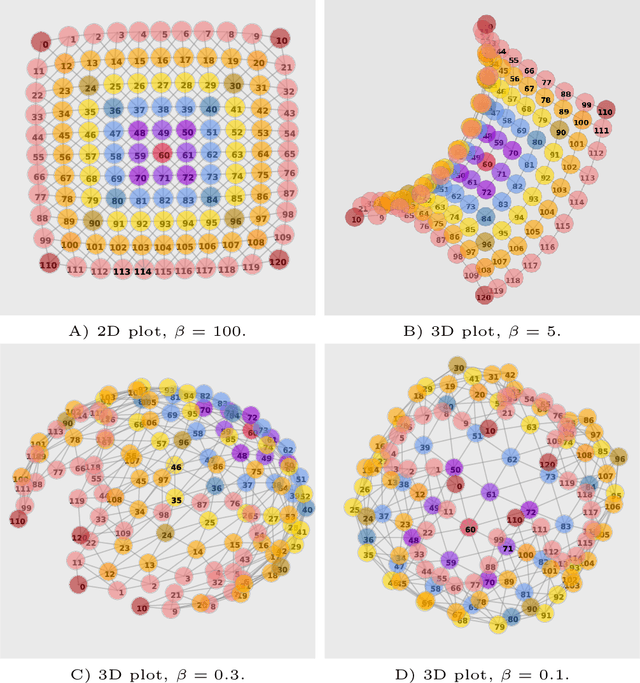
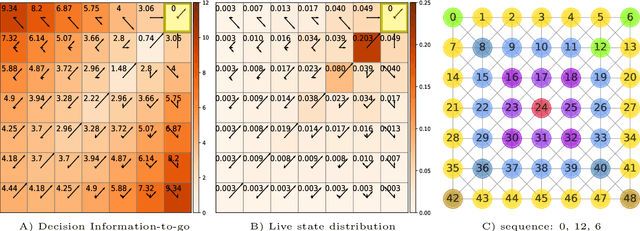
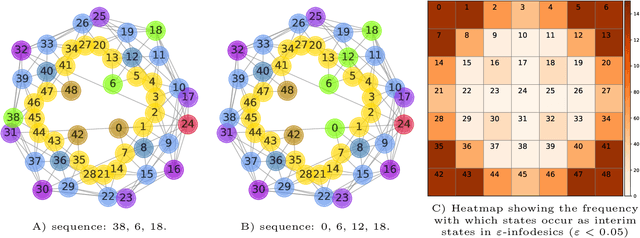
Traditionally, Euclidean geometry is treated by scientists as a priori and objective. However, when we take the position of an agent, the problem of selecting a best route should also factor in the abilities of the agent, its embodiment and particularly its cognitive effort. In this paper we consider geometry in terms of travel between states within a world by incorporating information processing costs with the appropriate spatial distances. This induces a geometry that increasingly differs from the original geometry of the given world, as information costs become increasingly important. We visualize this \textit{"cognitive geometry"} by projecting it onto 2- and 3-dimensional spaces showing distinct distortions reflecting the emergence of epistemic and information-saving strategies as well as pivot states. The analogies between traditional cost-based geometries and those induced by additional informational costs invite a generalization of the traditional notion of geodesics as cheapest routes towards the notion of \textit{infodesics}. Crucially, the concept of infodesics approximates the usual geometric property that, travelling from a start to a goal along a geodesic, not only the goal, but all intermediate points are equally visited at optimal cost from the start.