A space of goals: the cognitive geometry of informationally bounded agents
Paper and Code
Nov 05, 2021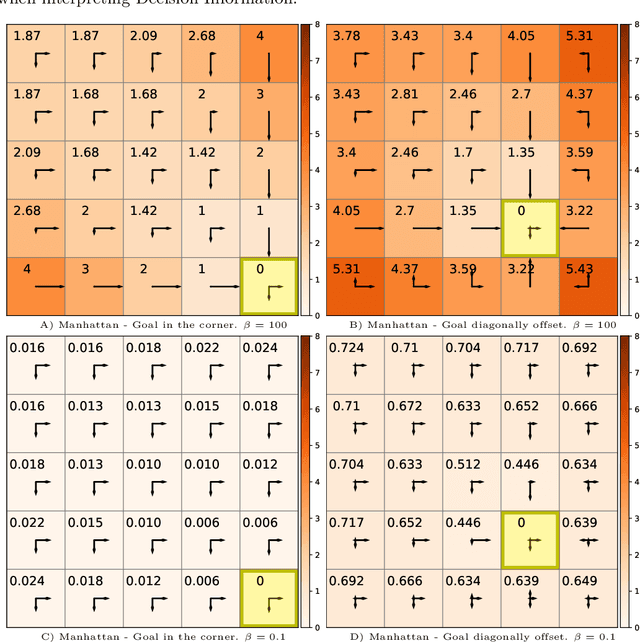
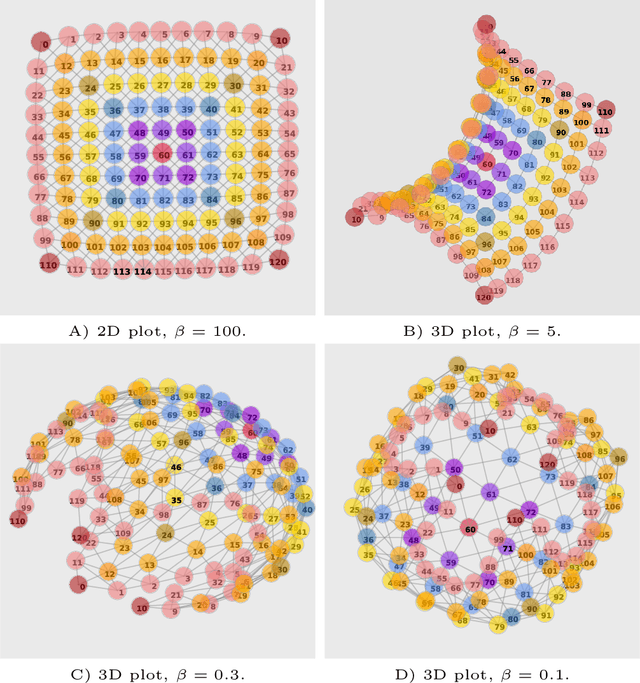
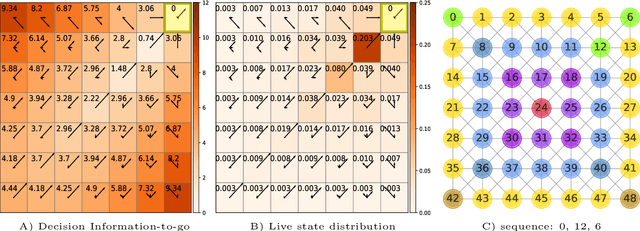
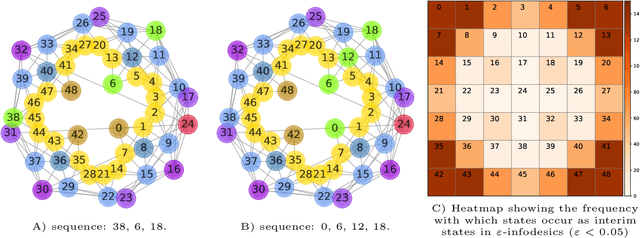
Traditionally, Euclidean geometry is treated by scientists as a priori and objective. However, when we take the position of an agent, the problem of selecting a best route should also factor in the abilities of the agent, its embodiment and particularly its cognitive effort. In this paper we consider geometry in terms of travel between states within a world by incorporating information processing costs with the appropriate spatial distances. This induces a geometry that increasingly differs from the original geometry of the given world, as information costs become increasingly important. We visualize this \textit{"cognitive geometry"} by projecting it onto 2- and 3-dimensional spaces showing distinct distortions reflecting the emergence of epistemic and information-saving strategies as well as pivot states. The analogies between traditional cost-based geometries and those induced by additional informational costs invite a generalization of the traditional notion of geodesics as cheapest routes towards the notion of \textit{infodesics}. Crucially, the concept of infodesics approximates the usual geometric property that, travelling from a start to a goal along a geodesic, not only the goal, but all intermediate points are equally visited at optimal cost from the start.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge