A Quasi-Newton Approach to Nonsmooth Convex Optimization Problems in Machine Learning

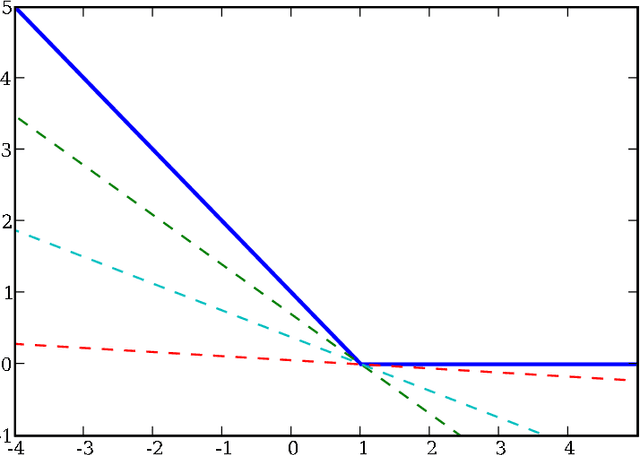
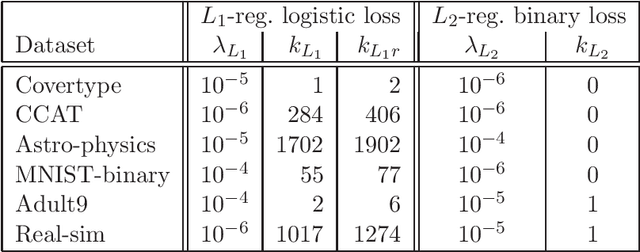
We extend the well-known BFGS quasi-Newton method and its memory-limited variant LBFGS to the optimization of nonsmooth convex objectives. This is done in a rigorous fashion by generalizing three components of BFGS to subdifferentials: the local quadratic model, the identification of a descent direction, and the Wolfe line search conditions. We prove that under some technical conditions, the resulting subBFGS algorithm is globally convergent in objective function value. We apply its memory-limited variant (subLBFGS) to L_2-regularized risk minimization with the binary hinge loss. To extend our algorithm to the multiclass and multilabel settings, we develop a new, efficient, exact line search algorithm. We prove its worst-case time complexity bounds, and show that our line search can also be used to extend a recently developed bundle method to the multiclass and multilabel settings. We also apply the direction-finding component of our algorithm to L_1-regularized risk minimization with logistic loss. In all these contexts our methods perform comparable to or better than specialized state-of-the-art solvers on a number of publicly available datasets. An open source implementation of our algorithms is freely available.

Efficient Exact Inference in Planar Ising Models

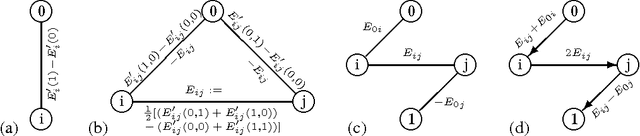
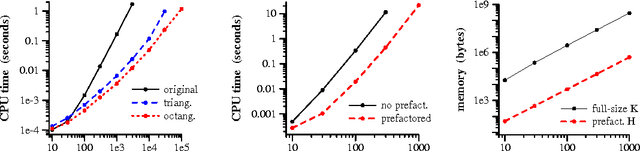
We give polynomial-time algorithms for the exact computation of lowest-energy (ground) states, worst margin violators, log partition functions, and marginal edge probabilities in certain binary undirected graphical models. Our approach provides an interesting alternative to the well-known graph cut paradigm in that it does not impose any submodularity constraints; instead we require planarity to establish a correspondence with perfect matchings (dimer coverings) in an expanded dual graph. We implement a unified framework while delegating complex but well-understood subproblems (planar embedding, maximum-weight perfect matching) to established algorithms for which efficient implementations are freely available. Unlike graph cut methods, we can perform penalized maximum-likelihood as well as maximum-margin parameter estimation in the associated conditional random fields (CRFs), and employ marginal posterior probabilities as well as maximum a posteriori (MAP) states for prediction. Maximum-margin CRF parameter estimation on image denoising and segmentation problems shows our approach to be efficient and effective. A C++ implementation is available from http://nic.schraudolph.org/isinf/

Graph Kernels

We present a unified framework to study graph kernels, special cases of which include the random walk graph kernel \citep{GaeFlaWro03,BorOngSchVisetal05}, marginalized graph kernel \citep{KasTsuIno03,KasTsuIno04,MahUedAkuPeretal04}, and geometric kernel on graphs \citep{Gaertner02}. Through extensions of linear algebra to Reproducing Kernel Hilbert Spaces (RKHS) and reduction to a Sylvester equation, we construct an algorithm that improves the time complexity of kernel computation from $O(n^6)$ to $O(n^3)$. When the graphs are sparse, conjugate gradient solvers or fixed-point iterations bring our algorithm into the sub-cubic domain. Experiments on graphs from bioinformatics and other application domains show that it is often more than a thousand times faster than previous approaches. We then explore connections between diffusion kernels \citep{KonLaf02}, regularization on graphs \citep{SmoKon03}, and graph kernels, and use these connections to propose new graph kernels. Finally, we show that rational kernels \citep{CorHafMoh02,CorHafMoh03,CorHafMoh04} when specialized to graphs reduce to the random walk graph kernel.