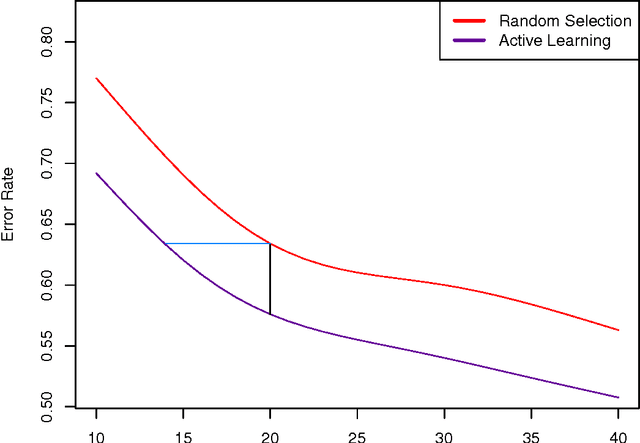
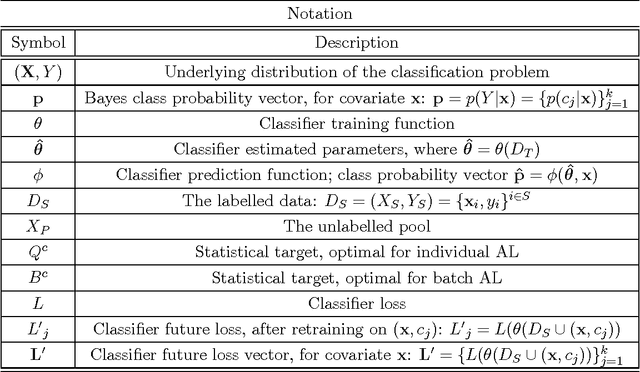
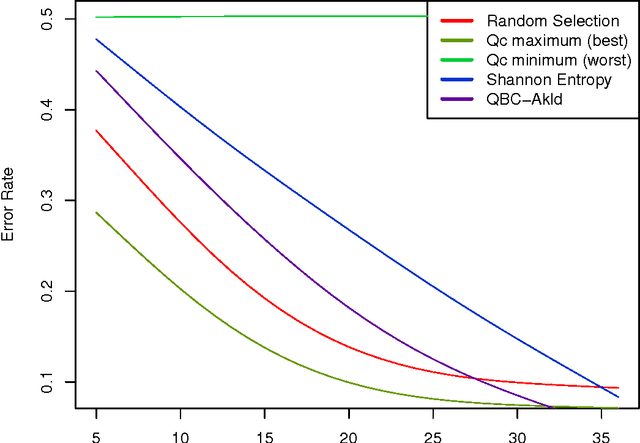
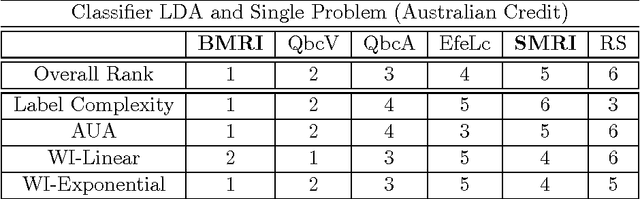
Estimating Optimal Active Learning via Model Retraining Improvement

A central question for active learning (AL) is: "what is the optimal selection?" Defining optimality by classifier loss produces a new characterisation of optimal AL behaviour, by treating expected loss reduction as a statistical target for estimation. This target forms the basis of model retraining improvement (MRI), a novel approach providing a statistical estimation framework for AL. This framework is constructed to address the central question of AL optimality, and to motivate the design of estimation algorithms. MRI allows the exploration of optimal AL behaviour, and the examination of AL heuristics, showing precisely how they make sub-optimal selections. The abstract formulation of MRI is used to provide a new guarantee for AL, that an unbiased MRI estimator should outperform random selection. This MRI framework reveals intricate estimation issues that in turn motivate the construction of new statistical AL algorithms. One new algorithm in particular performs strongly in a large-scale experimental study, compared to standard AL methods. This competitive performance suggests that practical efforts to minimise estimation bias may be important for AL applications.

When does Active Learning Work?

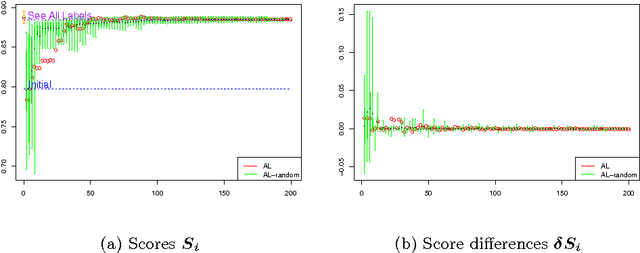
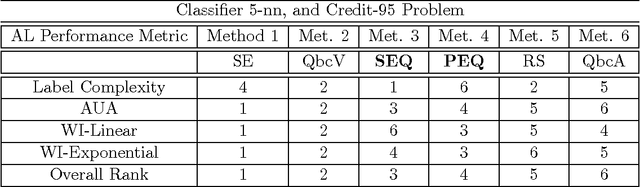
Active Learning (AL) methods seek to improve classifier performance when labels are expensive or scarce. We consider two central questions: Where does AL work? How much does it help? To address these questions, a comprehensive experimental simulation study of Active Learning is presented. We consider a variety of tasks, classifiers and other AL factors, to present a broad exploration of AL performance in various settings. A precise way to quantify performance is needed in order to know when AL works. Thus we also present a detailed methodology for tackling the complexities of assessing AL performance in the context of this experimental study.

Targeting Optimal Active Learning via Example Quality

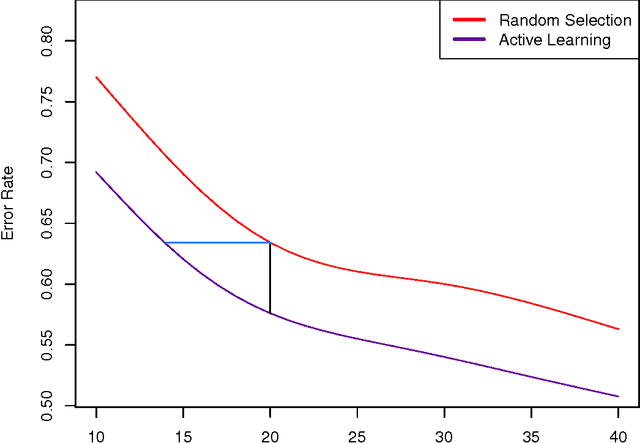
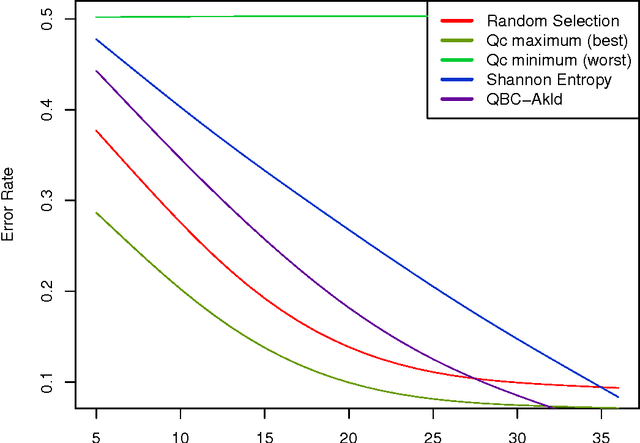
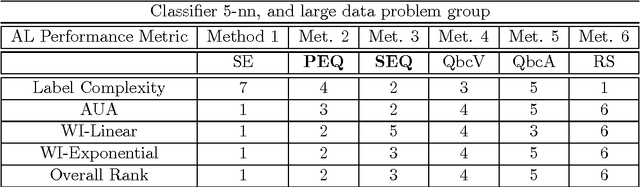
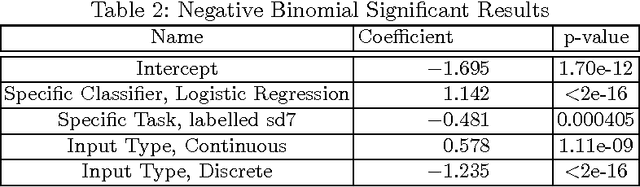
In many classification problems unlabelled data is abundant and a subset can be chosen for labelling. This defines the context of active learning (AL), where methods systematically select that subset, to improve a classifier by retraining. Given a classification problem, and a classifier trained on a small number of labelled examples, consider the selection of a single further example. This example will be labelled by the oracle and then used to retrain the classifier. This example selection raises a central question: given a fully specified stochastic description of the classification problem, which example is the optimal selection? If optimality is defined in terms of loss, this definition directly produces expected loss reduction (ELR), a central quantity whose maximum yields the optimal example selection. This work presents a new theoretical approach to AL, example quality, which defines optimal AL behaviour in terms of ELR. Once optimal AL behaviour is defined mathematically, reasoning about this abstraction provides insights into AL. In a theoretical context the optimal selection is compared to existing AL methods, showing that heuristics can make sub-optimal selections. Algorithms are constructed to estimate example quality directly. A large-scale experimental study shows these algorithms to be competitive with standard AL methods.

Exponentially Weighted Moving Average Charts for Detecting Concept Drift

Classifying streaming data requires the development of methods which are computationally efficient and able to cope with changes in the underlying distribution of the stream, a phenomenon known in the literature as concept drift. We propose a new method for detecting concept drift which uses an Exponentially Weighted Moving Average (EWMA) chart to monitor the misclassification rate of an streaming classifier. Our approach is modular and can hence be run in parallel with any underlying classifier to provide an additional layer of concept drift detection. Moreover our method is computationally efficient with overhead O(1) and works in a fully online manner with no need to store data points in memory. Unlike many existing approaches to concept drift detection, our method allows the rate of false positive detections to be controlled and kept constant over time.