Nelvin Tan
Improved Evidence Extraction for Document Inconsistency Detection with LLMs
Jan 06, 2026Abstract:Large language models (LLMs) are becoming useful in many domains due to their impressive abilities that arise from large training datasets and large model sizes. However, research on LLM-based approaches to document inconsistency detection is relatively limited. There are two key aspects of document inconsistency detection: (i) classification of whether there exists any inconsistency, and (ii) providing evidence of the inconsistent sentences. We focus on the latter, and introduce new comprehensive evidence-extraction metrics and a redact-and-retry framework with constrained filtering that substantially improves LLM-based document inconsistency detection over direct prompting. We back our claims with promising experimental results.
Improved LLM Agents for Financial Document Question Answering
Jun 10, 2025
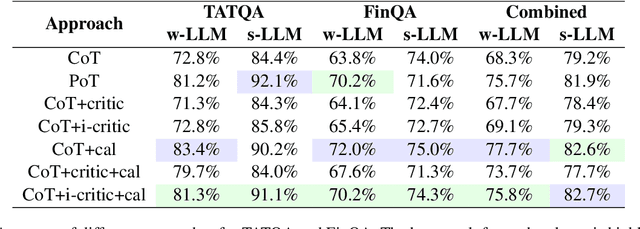
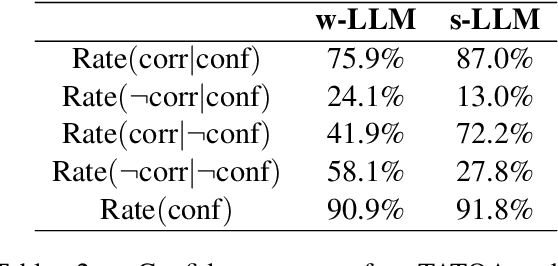
Abstract:Large language models (LLMs) have shown impressive capabilities on numerous natural language processing tasks. However, LLMs still struggle with numerical question answering for financial documents that include tabular and textual data. Recent works have showed the effectiveness of critic agents (i.e., self-correction) for this task given oracle labels. Building upon this framework, this paper examines the effectiveness of the traditional critic agent when oracle labels are not available, and show, through experiments, that this critic agent's performance deteriorates in this scenario. With this in mind, we present an improved critic agent, along with the calculator agent which outperforms the previous state-of-the-art approach (program-of-thought) and is safer. Furthermore, we investigate how our agents interact with each other, and how this interaction affects their performance.
Flexible and Efficient Drift Detection without Labels
Jun 10, 2025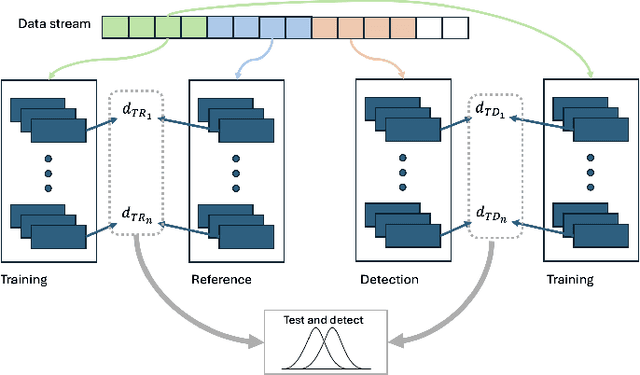
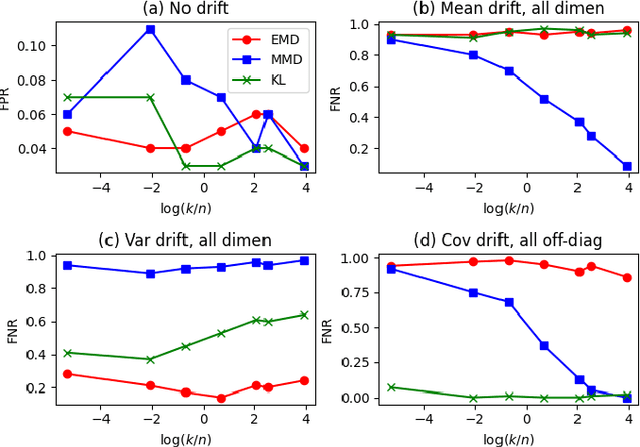
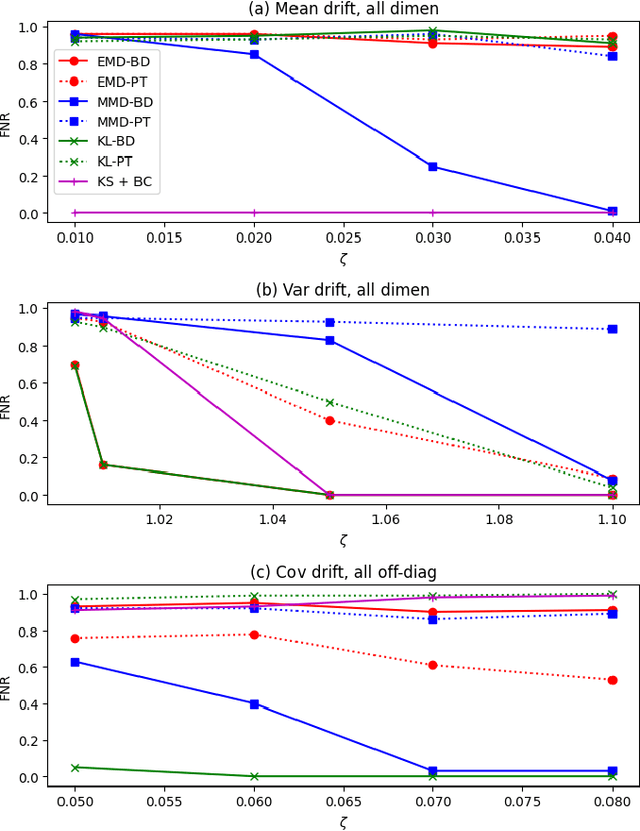
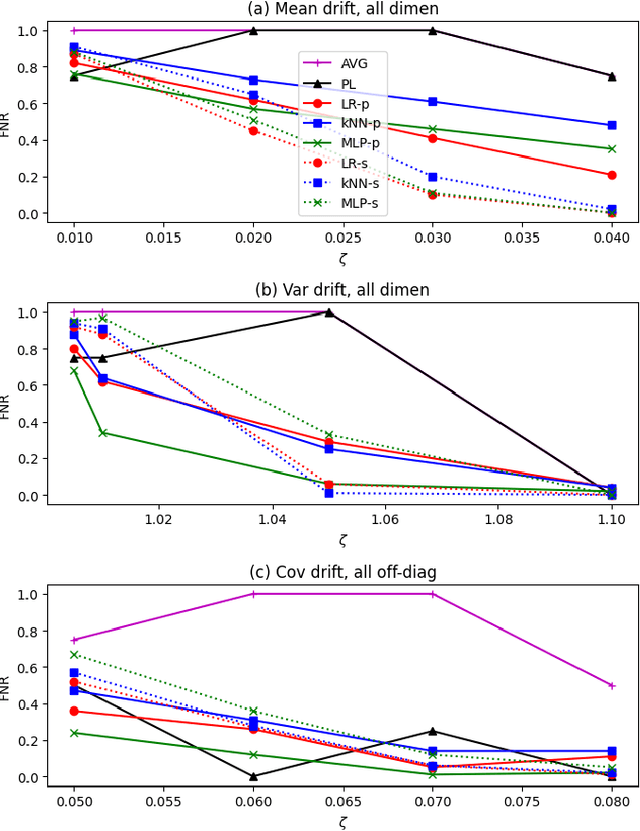
Abstract:Machine learning models are being increasingly used to automate decisions in almost every domain, and ensuring the performance of these models is crucial for ensuring high quality machine learning enabled services. Ensuring concept drift is detected early is thus of the highest importance. A lot of research on concept drift has focused on the supervised case that assumes the true labels of supervised tasks are available immediately after making predictions. Controlling for false positives while monitoring the performance of predictive models used to make inference from extremely large datasets periodically, where the true labels are not instantly available, becomes extremely challenging. We propose a flexible and efficient concept drift detection algorithm that uses classical statistical process control in a label-less setting to accurately detect concept drifts. We shown empirically that under computational constraints, our approach has better statistical power than previous known methods. Furthermore, we introduce a new drift detection framework to model the scenario of detecting drift (without labels) given prior detections, and show our how our drift detection algorithm can be incorporated effectively into this framework. We demonstrate promising performance via numerical simulations.
Quantitative Group Testing and Pooled Data in the Linear Regime with Sublinear Tests
Aug 01, 2024Abstract:In the pooled data problem, the goal is to identify the categories associated with a large collection of items via a sequence of pooled tests. Each pooled test reveals the number of items in the pool belonging to each category. A prominent special case is quantitative group testing (QGT), which is the case of pooled data with two categories. We consider these problems in the non-adaptive and linear regime, where the fraction of items in each category is of constant order. We propose a scheme with a spatially coupled Bernoulli test matrix and an efficient approximate message passing (AMP) algorithm for recovery. We rigorously characterize its asymptotic performance in both the noiseless and noisy settings, and prove that in the noiseless case, the AMP algorithm achieves almost-exact recovery with a number of tests sublinear in the number of items. For both QGT and pooled data, this is the first efficient scheme that provably achieves recovery in the linear regime with a sublinear number of tests, with performance degrading gracefully in the presence of noise. Numerical simulations illustrate the benefits of the spatially coupled scheme at finite dimensions, showing that it outperforms i.i.d. test designs as well as other recovery algorithms based on convex programming.
Approximate Message Passing with Rigorous Guarantees for Pooled Data and Quantitative Group Testing
Sep 27, 2023Abstract:In the pooled data problem, the goal is to identify the categories associated with a large collection of items via a sequence of pooled tests. Each pooled test reveals the number of items of each category within the pool. We study an approximate message passing (AMP) algorithm for estimating the categories and rigorously characterize its performance, in both the noiseless and noisy settings. For the noiseless setting, we show that the AMP algorithm is equivalent to one recently proposed by El Alaoui et al. Our results provide a rigorous version of their performance guarantees, previously obtained via non-rigorous techniques. For the case of pooled data with two categories, known as quantitative group testing (QGT), we use the AMP guarantees to compute precise limiting values of the false positive rate and the false negative rate. Though the pooled data problem and QGT are both instances of estimation in a linear model, existing AMP theory cannot be directly applied since the design matrices are binary valued. The key technical ingredient in our result is a rigorous analysis of AMP for generalized linear models defined via generalized white noise design matrices. This result, established using a recent universality result of Wang et al., is of independent interest. Our theoretical results are validated by numerical simulations. For comparison, we propose estimators based on convex relaxation and iterative thresholding, without providing theoretical guarantees. Our simulations indicate that AMP outperforms the convex programming estimator for a range of QGT scenarios, but the convex program performs better for pooled data with three categories.
Mixed Regression via Approximate Message Passing
Apr 05, 2023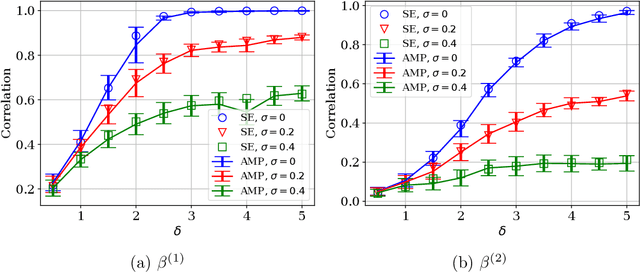
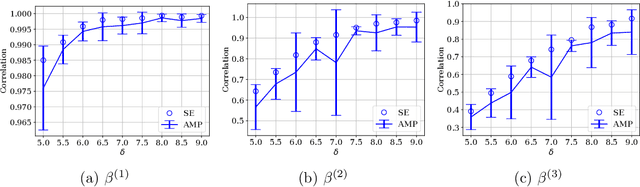
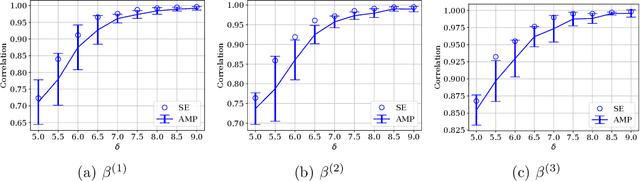
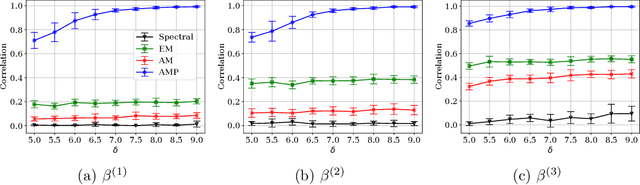
Abstract:We study the problem of regression in a generalized linear model (GLM) with multiple signals and latent variables. This model, which we call a matrix GLM, covers many widely studied problems in statistical learning, including mixed linear regression, max-affine regression, and mixture-of-experts. In mixed linear regression, each observation comes from one of $L$ signal vectors (regressors), but we do not know which one; in max-affine regression, each observation comes from the maximum of $L$ affine functions, each defined via a different signal vector. The goal in all these problems is to estimate the signals, and possibly some of the latent variables, from the observations. We propose a novel approximate message passing (AMP) algorithm for estimation in a matrix GLM and rigorously characterize its performance in the high-dimensional limit. This characterization is in terms of a state evolution recursion, which allows us to precisely compute performance measures such as the asymptotic mean-squared error. The state evolution characterization can be used to tailor the AMP algorithm to take advantage of any structural information known about the signals. Using state evolution, we derive an optimal choice of AMP `denoising' functions that minimizes the estimation error in each iteration. The theoretical results are validated by numerical simulations for mixed linear regression, max-affine regression, and mixture-of-experts. For max-affine regression, we propose an algorithm that combines AMP with expectation-maximization to estimate intercepts of the model along with the signals. The numerical results show that AMP significantly outperforms other estimators for mixed linear regression and max-affine regression in most parameter regimes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge