Nejat Arınık
CRIL
Whole-Graph Representation Learning For the Classification of Signed Networks
Sep 30, 2024
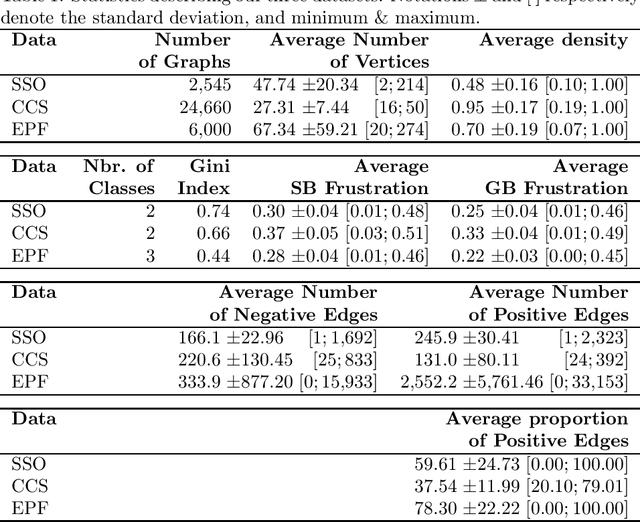
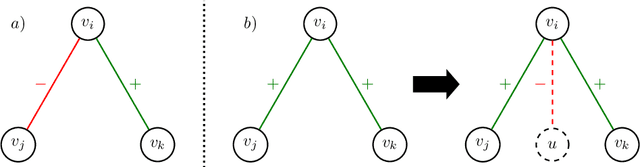

Abstract:Graphs are ubiquitous for modeling complex systems involving structured data and relationships. Consequently, graph representation learning, which aims to automatically learn low-dimensional representations of graphs, has drawn a lot of attention in recent years. The overwhelming majority of existing methods handle unsigned graphs. However, signed graphs appear in an increasing number of application domains to model systems involving two types of opposed relationships. Several authors took an interest in signed graphs and proposed methods for providing vertex-level representations, but only one exists for whole-graph representations, and it can handle only fully connected graphs. In this article, we tackle this issue by proposing two approaches to learning whole-graph representations of general signed graphs. The first is a SG2V, a signed generalization of the whole-graph embedding method Graph2vec that relies on a modification of the Weisfeiler--Lehman relabelling procedure. The second one is WSGCN, a whole-graph generalization of the signed vertex embedding method SGCN that relies on the introduction of master nodes into the GCN. We propose several variants of both these approaches. A bottleneck in the development of whole-graph-oriented methods is the lack of data. We constitute a benchmark composed of three collections of signed graphs with corresponding ground truths. We assess our methods on this benchmark, and our results show that the signed whole-graph methods learn better representations for this task. Overall, the baseline obtains an F-measure score of 58.57, when SG2V and WSGCN reach 73.01 and 81.20, respectively. Our source code and benchmark dataset are both publicly available online.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge