Self-guided Approximate Linear Programs

Approximate linear programs (ALPs) are well-known models based on value function approximations (VFAs) to obtain heuristic policies and lower bounds on the optimal policy cost of Markov decision processes (MDPs). The ALP VFA is a linear combination of predefined basis functions that are chosen using domain knowledge and updated heuristically if the ALP optimality gap is large. We side-step the need for such basis function engineering in ALP -- an implementation bottleneck -- by proposing a sequence of ALPs that embed increasing numbers of random basis functions obtained via inexpensive sampling. We provide a sampling guarantee and show that the VFAs from this sequence of models converge to the exact value function. Nevertheless, the performance of the ALP policy can fluctuate significantly as more basis functions are sampled. To mitigate these fluctuations, we "self-guide" our convergent sequence of ALPs using past VFA information such that a worst-case measure of policy performance is improved. We perform numerical experiments on perishable inventory control and generalized joint replenishment applications, which, respectively, give rise to challenging discounted-cost MDPs and average-cost semi-MDPs. We find that self-guided ALPs (i) significantly reduce policy cost fluctuations and improve the optimality gaps from an ALP approach that employs basis functions tailored to the former application, and (ii) deliver optimality gaps that are comparable to a known adaptive basis function generation approach targeting the latter application. More broadly, our methodology provides application-agnostic policies and lower bounds to benchmark approaches that exploit application structure.

A Data Efficient and Feasible Level Set Method for Stochastic Convex Optimization with Expectation Constraints

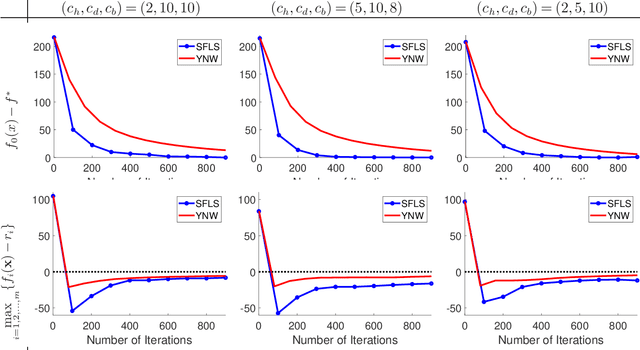
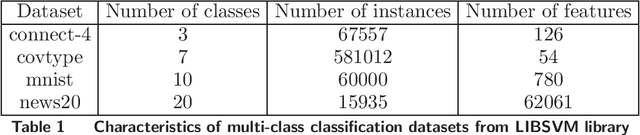
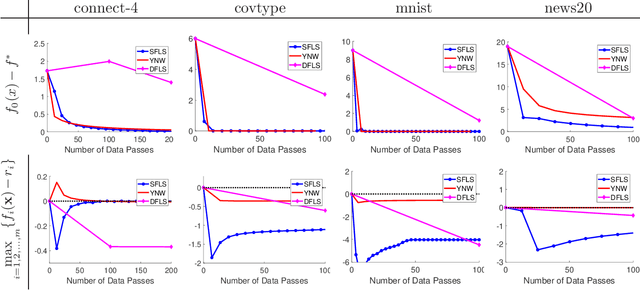
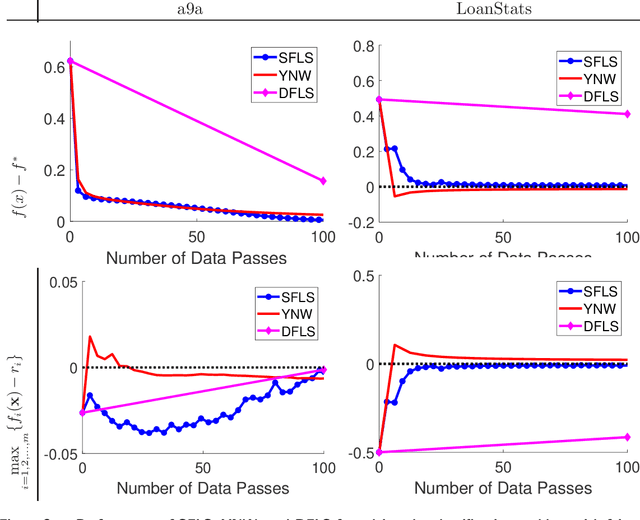
Stochastic convex optimization problems with expectation constraints (SOECs) are encountered in statistics and machine learning, business, and engineering. In data-rich environments, the SOEC objective and constraints contain expectations defined with respect to large datasets. Therefore, efficient algorithms for solving such SOECs need to limit the fraction of data points that they use, which we refer to as algorithmic data complexity. Recent stochastic first order methods exhibit low data complexity when handling SOECs but guarantee near-feasibility and near-optimality only at convergence. These methods may thus return highly infeasible solutions when heuristically terminated, as is often the case, due to theoretical convergence criteria being highly conservative. This issue limits the use of first order methods in several applications where the SOEC constraints encode implementation requirements. We design a stochastic feasible level set method (SFLS) for SOECs that has low data complexity and emphasizes feasibility before convergence. Specifically, our level-set method solves a root-finding problem by calling a novel first order oracle that computes a stochastic upper bound on the level-set function by extending mirror descent and online validation techniques. We establish that SFLS maintains a high-probability feasible solution at each root-finding iteration and exhibits favorable iteration complexity compared to state-of-the-art deterministic feasible level set and stochastic subgradient methods. Numerical experiments on three diverse applications validate the low data complexity of SFLS relative to the former approach and highlight how SFLS finds feasible solutions with small optimality gaps significantly faster than the latter method.