Neal Gafter
Coarsening Optimization for Differentiable Programming
Oct 05, 2021
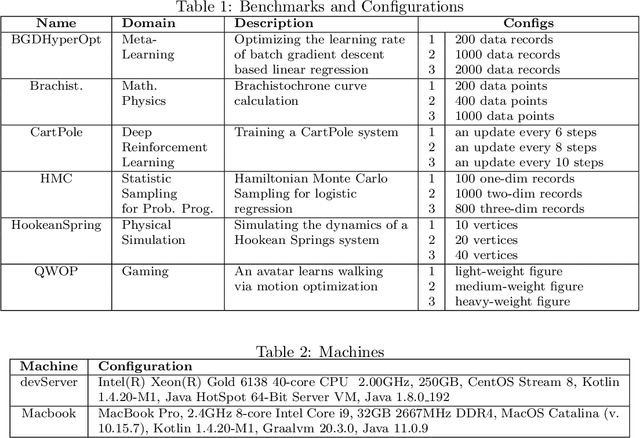
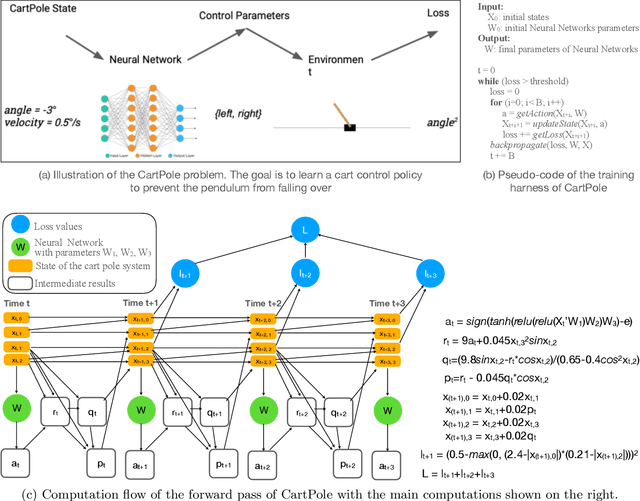

Abstract:This paper presents a novel optimization for differentiable programming named coarsening optimization. It offers a systematic way to synergize symbolic differentiation and algorithmic differentiation (AD). Through it, the granularity of the computations differentiated by each step in AD can become much larger than a single operation, and hence lead to much reduced runtime computations and data allocations in AD. To circumvent the difficulties that control flow creates to symbolic differentiation in coarsening, this work introduces phi-calculus, a novel method to allow symbolic reasoning and differentiation of computations that involve branches and loops. It further avoids "expression swell" in symbolic differentiation and balance reuse and coarsening through the design of reuse-centric segment of interest identification. Experiments on a collection of real-world applications show that coarsening optimization is effective in speeding up AD, producing several times to two orders of magnitude speedups.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge