A Machine Learning Framework for Real-time Inverse Modeling and Multi-objective Process Optimization of Composites for Active Manufacturing Control

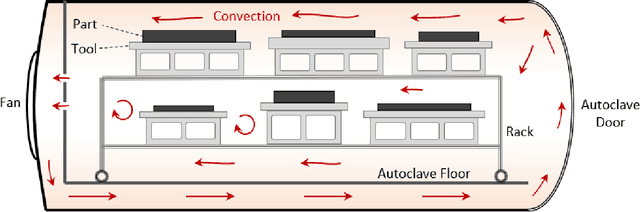
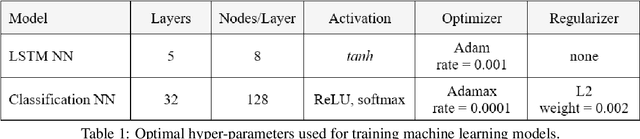
For manufacturing of aerospace composites, several parts may be processed simultaneously using convective heating in an autoclave. Due to uncertainties including tool placement, convective Boundary Conditions (BCs) vary in each run. As a result, temperature histories in some of the parts may not conform to process specifications due to under-curing or over-heating. Thermochemical analysis using Finite Element (FE) simulations are typically conducted prior to fabrication based on assumed range of BCs. This, however, introduces unnecessary constraints on the design. To monitor the process, thermocouples (TCs) are placed under tools near critical locations. The TC data may be used to back-calculate BCs using trial-and-error FE analysis. However, since the inverse heat transfer problem is ill-posed, many solutions are obtained for given TC data. In this study, a novel machine learning (ML) framework is presented capable of optimizing air temperature cycle in real-time based on TC data from multiple parts, for active control of manufacturing. The framework consists of two recurrent Neural Networks (NN) for inverse modeling of the ill-posed curing problem at the speed of 300 simulations/second, and a classification NN for multi-objective optimization of the air temperature at the speed of 35,000 simulations/second. A virtual demonstration of the framework for process optimization of three composite parts with data from three TCs is presented.

Theory-Guided Machine Learning for Process Simulation of Advanced Composites

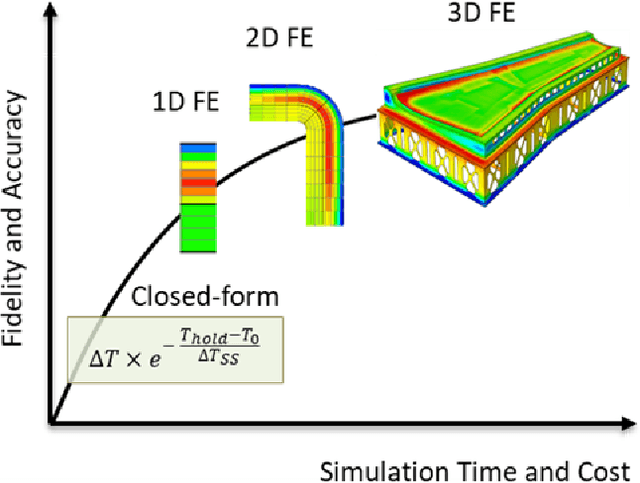
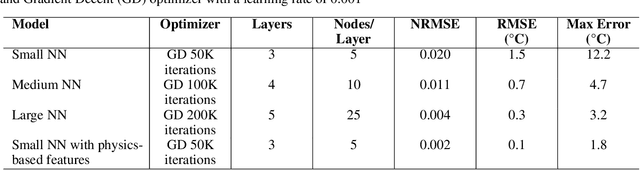
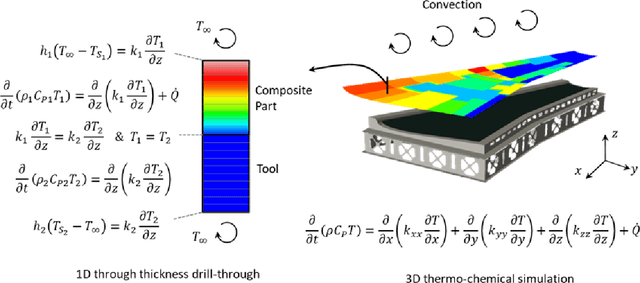
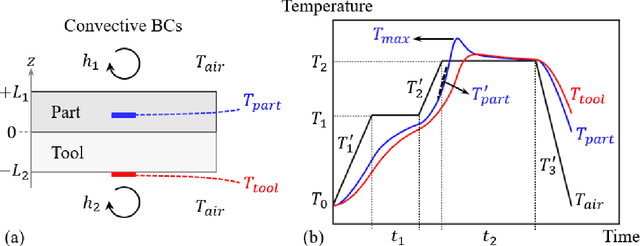
Science-based simulation tools such as Finite Element (FE) models are routinely used in scientific and engineering applications. While their success is strongly dependent on our understanding of underlying governing physical laws, they suffer inherent limitations including trade-off between fidelity/accuracy and speed. The recent rise of Machine Learning (ML) proposes a theory-agnostic paradigm. In complex multi-physics problems, however, creating large enough datasets for successful training of ML models has proven to be challenging. One promising strategy to bridge the divide between these approaches and take advantage of their respective strengths is Theory-Guided Machine Learning (TGML) which aims to integrate physical laws into ML algorithms. In this paper, three case studies on thermal management during processing of advanced composites are presented and studied using FE, ML and TGML. A structured approach to incrementally adding increasingly complex physics to training of TGML model is presented. The benefits of TGML over ML models are seen in more accurate predictions, particularly outside the training region, and ability to train with small datasets. One benefit of TGML over FE is significant speed improvement to potentially develop real-time feedback systems. A recent successful implementation of a TGML model to assess producibility of aerospace composite parts is presented.

A Physics-Informed Machine Learning Approach for Solving Heat Transfer Equation in Advanced Manufacturing and Engineering Applications

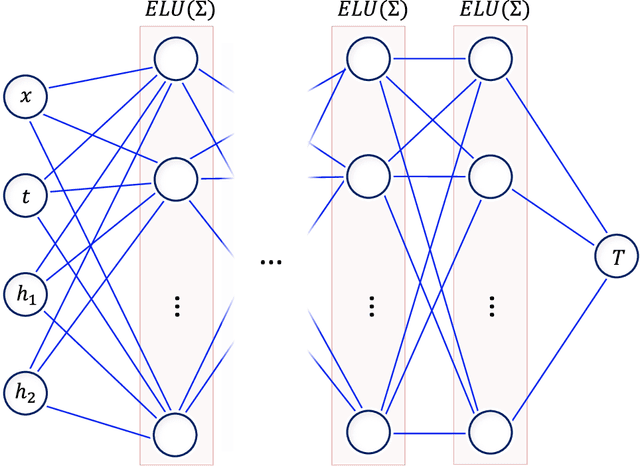
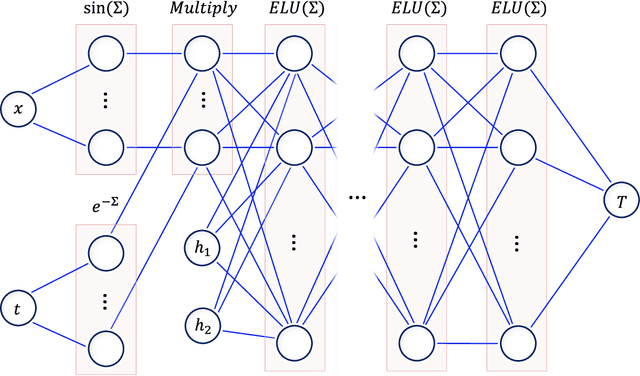
A physics-informed neural network is developed to solve conductive heat transfer partial differential equation (PDE), along with convective heat transfer PDEs as boundary conditions (BCs), in manufacturing and engineering applications where parts are heated in ovens. Since convective coefficients are typically unknown, current analysis approaches based on trial and error finite element (FE) simulations are slow. The loss function is defined based on errors to satisfy PDE, BCs and initial condition. An adaptive normalizing scheme is developed to reduce loss terms simultaneously. In addition, theory of heat transfer is used for feature engineering. The predictions for 1D and 2D cases are validated by comparing with FE results. It is shown that using engineered features, heat transfer beyond the training zone can be predicted. Trained model allows for fast evaluation of a range of BCs to develop feedback loops, realizing Industry 4.0 concept of active manufacturing control based on sensor data.

An Iterative Scientific Machine Learning Approach for Discovery of Theories Underlying Physical Phenomena

Form a pure mathematical point of view, common functional forms representing different physical phenomena can be defined. For example, rates of chemical reactions, diffusion and heat transfer are all governed by exponential-type expressions. If machine learning is used for physical problems, inferred from domain knowledge, original features can be transformed in such a way that the end expressions are highly aligned and correlated with the underlying physics. This should significantly reduce the training effort in terms of iterations, architecture and the number of required data points. We extend this by approaching a problem from an agnostic position and propose a systematic and iterative methodology to discover theories underlying physical phenomena. At first, commonly observed functional forms of theoretical expressions are used to transform original features before conducting correlation analysis to output. Using random combinations of highly correlated expressions, training of Neural Networks (NN) are performed. By comparing the rates of convergence or mean error in training, expressions describing the underlying physical problems can be discovered, leading to extracting explicit analytic equations. This approach was used in three blind demonstrations for different physical phenomena.