Model Approximation Using Cascade of Tree Decompositions

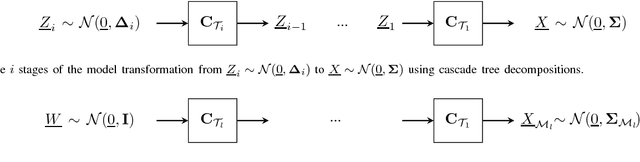
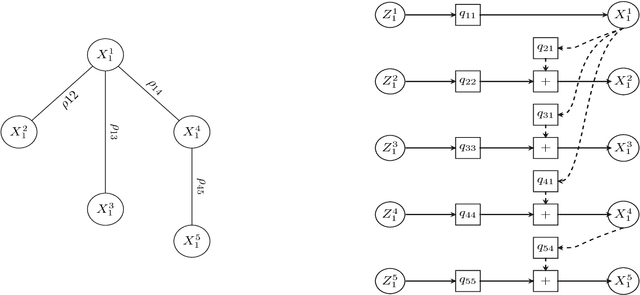
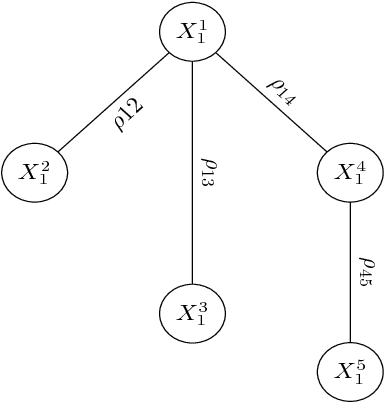
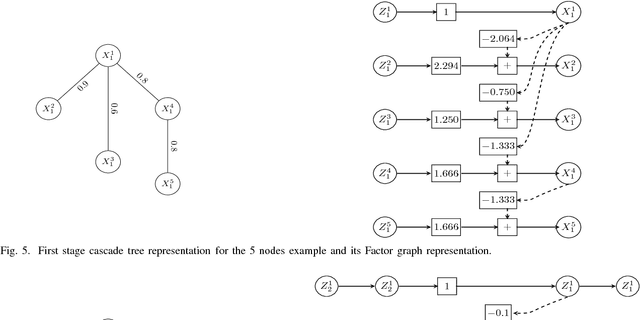
In this paper, we present a general, multistage framework for graphical model approximation using a cascade of models such as trees. In particular, we look at the problem of covariance matrix approximation for Gaussian distributions as linear transformations of tree models. This is a new way to decompose the covariance matrix. Here, we propose an algorithm which incorporates the Cholesky factorization method to compute the decomposition matrix and thus can approximate a simple graphical model using a cascade of the Cholesky factorization of the tree approximation transformations. The Cholesky decomposition enables us to achieve a tree structure factor graph at each cascade stage of the algorithm which facilitates the use of the message passing algorithm since the approximated graph has less loops compared to the original graph. The overall graph is a cascade of factor graphs with each factor graph being a tree. This is a different perspective on the approximation model, and algorithms such as Gaussian belief propagation can be used on this overall graph. Here, we present theoretical result that guarantees the convergence of the proposed model approximation using the cascade of tree decompositions. In the simulations, we look at synthetic and real data and measure the performance of the proposed framework by comparing the KL divergences.

The Quality of the Covariance Selection Through Detection Problem and AUC Bounds

We consider the problem of quantifying the quality of a model selection problem for a graphical model. We discuss this by formulating the problem as a detection problem. Model selection problems usually minimize a distance between the original distribution and the model distribution. For the special case of Gaussian distributions, the model selection problem simplifies to the covariance selection problem which is widely discussed in literature by Dempster [2] where the likelihood criterion is maximized or equivalently the Kullback-Leibler (KL) divergence is minimized to compute the model covariance matrix. While this solution is optimal for Gaussian distributions in the sense of the KL divergence, it is not optimal when compared with other information divergences and criteria such as Area Under the Curve (AUC). In this paper, we analytically compute upper and lower bounds for the AUC and discuss the quality of model selection problem using the AUC and its bounds as an accuracy measure in detection problem. We define the correlation approximation matrix (CAM) and show that analytical computation of the KL divergence, the AUC and its bounds only depend on the eigenvalues of CAM. We also show the relationship between the AUC, the KL divergence and the ROC curve by optimizing with respect to the ROC curve. In the examples provided, we pick tree structures as the simplest graphical models. We perform simulations on fully-connected graphs and compute the tree structured models by applying the widely used Chow-Liu algorithm [3]. Examples show that the quality of tree approximation models are not good in general based on information divergences, the AUC and its bounds when the number of nodes in the graphical model is large. We show both analytically and by simulations that the 1-AUC for the tree approximation model decays exponentially as the dimension of graphical model increases.