Model Approximation Using Cascade of Tree Decompositions
Paper and Code
Aug 10, 2018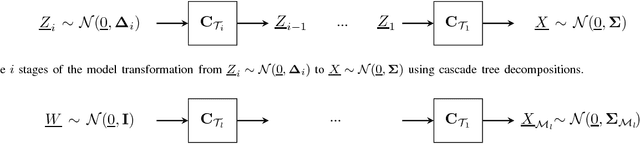
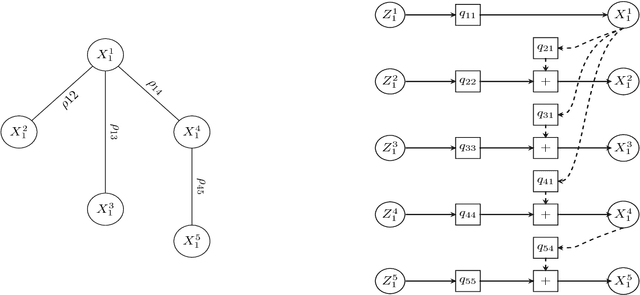
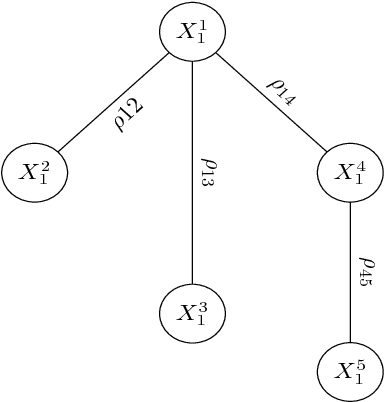
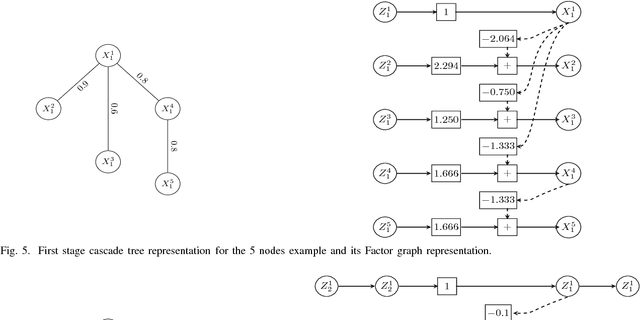
In this paper, we present a general, multistage framework for graphical model approximation using a cascade of models such as trees. In particular, we look at the problem of covariance matrix approximation for Gaussian distributions as linear transformations of tree models. This is a new way to decompose the covariance matrix. Here, we propose an algorithm which incorporates the Cholesky factorization method to compute the decomposition matrix and thus can approximate a simple graphical model using a cascade of the Cholesky factorization of the tree approximation transformations. The Cholesky decomposition enables us to achieve a tree structure factor graph at each cascade stage of the algorithm which facilitates the use of the message passing algorithm since the approximated graph has less loops compared to the original graph. The overall graph is a cascade of factor graphs with each factor graph being a tree. This is a different perspective on the approximation model, and algorithms such as Gaussian belief propagation can be used on this overall graph. Here, we present theoretical result that guarantees the convergence of the proposed model approximation using the cascade of tree decompositions. In the simulations, we look at synthetic and real data and measure the performance of the proposed framework by comparing the KL divergences.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge